Pensando tranquilamente el otro día mientras leía bajo la luz de mi lampara de escritorio con los tickers de bolsa moviéndose de un lado a otro en mi ordenador, se me ocurrió que una de las entradas que debía hacer era la de comunicar, de alguna manera, una forma de "mejorar" o "maximizar" la forma en la que podía transmitir la importancia del control de riesgos a la hora de crear una cartera de valores. Y evidentemente no se me podría haber ocurrido otra cosa que explicar de manera sencilla algo que ya muchos (supongo) sabréis, que es la diferencia existente que hay entre el riesgo sistemático y el no sistemático, así como la manera más inteligente de abordar el no sistemático, que a fin de cuentas es lo único que "controlamos". Procederé a mostrar un post lo más corto posible para no aburrir al personal, pero intentando ser lo más preciso posible, vayamos a ello.
TIPOS DE RIESGO BÁSICOS
La palabra "riesgo" es una palabra ciertamente engañosa. El riesgo puede ser muy diferentes según el tipo de inversor que seas, para un inversor cuantitativo el riesgo puede tener mucho que ver con la volatilidad del activo (y no solo cuantitativo, sino a nivel institucional también), sin embargo para un inversor Value el riesgo puede cobrar un tinte muy diferente. Desde mi punto de vista, considero que es bastante importante, sin embargo, entender que el riesgo tiene dos subdivisiones:
Riesgo Total = Riesgo sistemático + Riesgo NO sistemático
Tanto el sistemático como el no sistemático son dos riesgos diferentes que afectan de la misma manera a la cotización de un activo. Solo uno de ellos es inevitable.
- RIESGO SISTEMÁTICO: Al riesgo sistemático se le conoce como "riesgo de mercado" y está presente en todos los activos. Es el llamado riesgo inevitable y tiene mucho que ver con las expectativas de rentabilidad de los inversores sobre dicho activo.
- RIESGO NO SISTEMÁTICO: El riesgo no sistemático, por su lado, engloba todos aquellos factores propios de una empresa, digamos que su base es la incertidumbre de mercado y tienen mucho que ver con las "tripas" de dichas empresas. Por ejemplo, un riesgo no sistemático es que una empresa pierda un litigio, o que los resultados empresariales bajen año tras año, que se detecte fraude en sus cuentas etc. Este riesgo, al contrario que el anterior, SI es inevitable, veremos cómo.
EL PODER DE LA DIVERSIFICACIÓN
Aún recuerdo cuando leí hace mucho tiempo a Warren Buffet exponiendo algo así a que "si se tiene un buen conocimiento sobre lo que se está haciendo, diversificar es un error", menudo mito cayó aquel día...
La diversificación en cartera ha sido demostrada necesaria de manera sistemática año tras año, estudio tras estudio. Es de las pocas cosas/verdades a nivel financiero que ha sido capaz de mantenerse vigente a lo largo del tiempo y ha conseguido no solo mejorar los rendimientos en contra de las carteras menos diversificadas (hasta cierto nivel), sino evitar que muchos fondos colapsaran demasiado rápido. De hecho, si observamos al CAPM observamos algo muy similar a la descripción del problema que pretende solucionar la cultura de la diversificación: reducir el riesgo no sistemático.
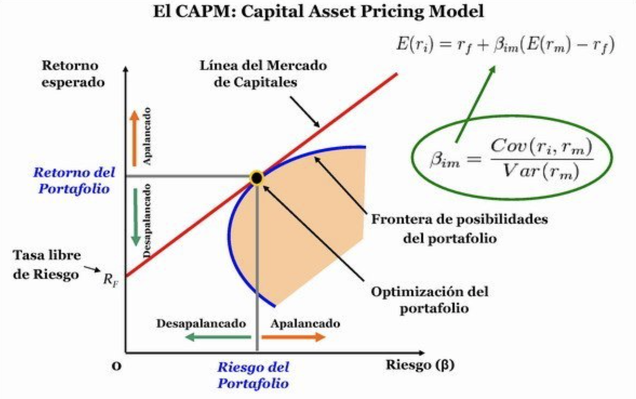
Y sí amigos, si nos fijamos en el modelo (el cual ya comenté en el post anterior que no es muy fiable que digamos porque parte de unas premisas equivocadas), aunque imperfecto, descubrimos que guarda una parte muy interesante en su formula. A saber que, la primera parte de la misma se refiere a la parte sistemática (rf) mientras que la segunda a la no sistemática (Bm(E(Rm)-rf)), y es esta, la segunda parte, la que no demuestra que la diversificación es capaz de reducir considerablemente el riesgo global, puesto que esta nos indica que necesita una Beta concreta. Esta beta, si la operamos según todos los modelos surgidos después de la teoría moderna de carteras (Markowitz), nos indica que a mas acciones tengamos en cartera, la beta de la misma cambiará según la interpelación no solo de las acciones con su mercado principal, sino entre ellas mismas. Y eh aquí la clave:
A la hora de reducir la beta de mercado, NO solo debemos elegir activos (de entre varios candidatos) con betas menores, sino que entre ellos, la sensibilidad correlativa sea lo menor posible.
En castellano: Si quieres tener una buena cartera de inversión, una vez tengas candidatos, no solo debes buscar acciones que tengan baja sensibilidad (Beta) con respecto a su activo de referencia, sino que también deben estar descorrelacionadas entre ellas, que sean independientes linealmente entre ellas.
CORRELACION Y CRITERIO DE INDEPENDENCIA LINEAL, CÓDIGO DE EJEMPLO
Obviamente no estoy descubriendo nada nuevo aquí, pero me gusta a veces recordar este tipo de premisas básicas a la hora de formar una cartera de inversión, puesto que a veces nos surge la duda de la descorrelación que pueda haber entre dos empresas. Además, muchas páginas por internet muestran las betas como si de algo mágico fuera, y lo cierto es que ese dato y nada es lo mismo, puesto que la beta suele variar mucho. Por ejemplo, un histórico de la evolución de la beta de Red eléctrica los últimos 10 años:
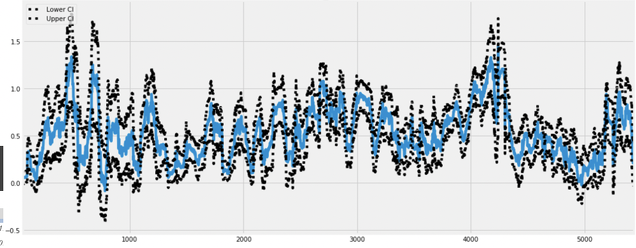
Entonces, ¿Qué nos queda?. Nos queda buscar las empresas lo más descorrelacinadas entre sí posible, por eso, y como decía en el párrafo anterior, es importante tener un abanico grande de candidatos a inversión. Por ejemplo, si queremos tener una cartera de 10 activos, y tenemos 15 candidatos, debemos coger de entre esos 15, los más descorrelacionados entre ellos, es decir, "más independientes linealmente hablando entre ellos a lo largo de una serie de valores (no en el momento actual)". Esto se suele hacer con matriz de varianzas covarianzas filtradas durante varios años o con otros métodos más específicos. Personalmente suelo usar paquetes en R o en Python para esta función, facilitan bastante la labor y hace que uno tome decisiones más rápido (al final del post os pongo el código de independencia lineal en el que de entre un conjunto de activos candidatos, este calcula los "x" valores (subtamaño) de dicho conjunto más independientes entre ellos, pero ojo que falta la carga de paquetes y de valores, tan solo os pongo el código de lo que hablamos en este post, puesto que tampoco esto es un blog de análisis cuantitativo, si alguien quiere el código íntegro que me lo comunique por privado), sin embargo mi máxima a la hora de aconsejar a amigos y gente que me pregunta y que no tiene conocimientos de programación o que no quieren complicarse la vida, suele ser la misma: Intenta maximizar la diversidad de sectores, países y tipos de empresas, a más diversificado entre aspectos empresariales (sector, país, materia prima etc), más probabilidades habrá de que exista una independencia lineal entre dichas empresas y, por consiguiente, más reducirás tu riesgo no sistemático.
Un saludo, y nos vemos en el próximo post!
CÓDIGO INDEPENDENCIA INTERCORRELATIVA:

Diversificar en el fondo es como no tener ni idea, si sabes algo o tienes un conocimiento de algo como dice Wuarren no tiene sentido diversificar ,,,
Es curioso después de escribirse tanto de mercados de teorías de venderse libros y cursos todo confluye en una sola cosa que es diversificar ....jajaja
Yo creo que diversificando no se hace dinero...
En respuesta a Pepe Mary Fer
ánimo con ello!
Diversificando no se hace dinero porque para diversificar lo tienes que tener y solo consigues obtener una rentabilidad a la que hay que restar la inflación ..
Porque todo son como vasos comunicantes se vacía uno y se llena otro luego con uno ganas y con otro pierdes...
A la larga te quedas igual , salvo que te jubiles en una cresta y des conferencias o a otros les toca un valle como a los Values ...jajaja
Hola,
Mi modesta opinión: Veo post y respuestas de distintos autores que confunden totalmente la Teoría de Carteras de Markowitz con el Modelo CAPM, y viceversa. Además, veo muchos post en los que no se entiende el concepto de aleatoriedad de las rentabilidades y eso les lleva a hacer una crítica al CAPM.
En primer lugar, la Tª de Carteras de Markowitz, identifica riesgo como la posibilidad de obtener una rentabilidad alejada de su valor esperado. Una buena medida para esta definició de riesgo es las varianza (o desviación típica). Pues en este marco, H.Markowitz demuestra que combinando activos con bajas correlaciones se pueden conseguir carteras con mejores combinaciones rentabilidad esperada/varianza que con activos individuales. Críticas hay muchas: "para mi la varianza no mide el riesgo; es un modelo estático, de un solo periodo, no es dinámico; se trata de un problema "ill-posed", en el que un pequeño cambio en las estimaciones hace que te cambie mucho la solución (esto no es bueno)". A pesar de todo esto, es innegable que la diversificación es casi el único "free-lunch" que hay en finanzas.
Respecto a la Tª de Carteras, yo creo que está más pensada para decisiones de asset allocation, para grandes familias de activos: RV Doméstica, RV Internacional, RV Emergente, RF Domestica a cp, RF Doméstica a lp, Commodities, REITs, etc... no está pensada para acciones individuales. ¿Porqué digo esto? porque los beneficios de la diversificación son mayores cuando menores son las correlaciones, y las correlaciones son menores entre clases de activos.
Respecto al CAPM, es un modelo económico (no un modelo matemático), en el que hay unos agentes que se supone que se comportan de una manera, hay una demanda y una oferta de títulos, y de ahí sale la composición de la cartera de activos arriesgados que comprarán todos los agentes de ese modelo: la cartera de mercado. El link entre Markowitz y el CAPM (el primero es de 1952 y el 2º es de 1964) está en que el CAPM asume que los agentes se comportan "alla Markowitz", es decir, toman decisiones óptimas basándose en la rentabilidad esperada y en la varianza de la rentabilidad. Pero quiero que quede claro que Markowitz sólo resuelve un problema matemático, una optimización. Digamos que el el modelo de Markowitz se puede leer/entender totalmente desprovisto de economía. El CAPM no.
Además, las respuestas que ofrecen ambos modelos/teorías son distintas. Markowitz nos dice como hallar los pesos óptimos de una cartera, mientras que el CAPM no dice nada de eso, nos dice cual es la rentabilidad esperada de los activos financieros.
Ahora llego al punto más criticado del CAPM: no sirve para predecir rentabilidades. La aplicación del CAPM nos devuelve una rentabilidad esperada de un activo financiero. Ahora lanzo esta pregunta: Si el CAPM se cumpliera, ¿deberiamos ver que la rentabilidad realizada de una acción o un índice fuese la que predecía el CAPM o siquiera un valor cercano? NO. ¿Obtener una rentabilidad muy alejada de la que se esperaba por CAPM invalida el modelo? NO. Por decirlo llanamente, la rentabilidad esperada (el output del CAPM) sólo nos informa de donde situar el "centro" de la distribución de probabilidad, el centro de la "campana". Lo que ocurre es que los activos financieros de renta variable tienen un varianza enorme comparada con los valores de rentabilidad esperada, y la rentabilidad esperada.
El problema se puede resumir así. Si obtengo valores aleatorios de una distribución normal (con mucha varianza) y están alejados de su valor esperado, ¿esto quiere decir que la media de distribución normal con la que he generado los números aleatorios es incorrecta? NO.
Perdón por el rollazo.
Saludos
En respuesta a Pedro Martinez
Primero de todo, gracias por la crítica, muy oportuna e interesante.
Por su lado, comentar que el error se debe a una mala redacción por mi parte, tiene usted toda la razón, mi referencia en relación al CAPM-T.Carteras es simplemente de marco, es decir, la teoría moderna tiene su base en el modelo propuesto por Markowitz, basado en el comportamiento racional del inversor, a partir de la cual se han desarrollado más teorías como el modelo diagonal de Sharpe o modelos de fijación de precios en equilibrio como el APT y... el CAPM. Mi intención no es hacer una interpretación de un CAPM embebido dentro de una teoría de carteras, mi intención es a nivel cronológico y de bases-desarrollos, pero tiene usted razón al matizar este aspecto, quizás tenga que corregir la manera de expresarme mejor cuando hablo de este tema. En cualquier caso me da usted una idea para hacer alguna entrada sobre la importancia del asset allocation (que desde mi punto de vista es lo más importante a nivel de finanzas, más incluso que escoger activos descorrelacionados)
En cuanto al modelo CAPM ya expresé mi opinión sobre el tema, la cual va en linea totalmente con la teoría fundamentada por Pablo Fernandez en Valoración de Empresas, aquí escribí un post sobre este aspecto en concreto:
https://inbestia.com/analisis/sobre-el-analisis-fundamental-y-los-monstruos-que-siguen-viniendo-a-verme
En esta linea también eché mano de artículos como:
https://hbr.org/1982/01/does-the-capital-asset-pricing-model-work
Donde se argumenta algo que iria, en parte, en linea con lo que argumenta: "Because of its shortcomings, financial executives should not rely on CAPM as a precise algorithm for estimating the cost of equity capital. Nevertheless, tests of the model confirm that it has much to say about the way returns are determined in financial markets. In view of the inherent difficulty in measuring the cost of equity, CAPM’s deficiencies appear no worse than those of other approaches. Its key advantage is that it quantifies risk and provides a widely applicable, relatively objective routine for translating risk measures into estimates of expected return.
En cualquier caso, gracias por el acertado comentario, las criticas constructivas son siempre bienvenidas.
Para aumentar la rentabilidad nos va mejor concentrarnos en ideas de alta convicción.
como el fondo Nomad que fue cerrado por sus gestores, en el 2013, recomendando invertir en Costco, Berkshire y Amazon.
Diversificando e incorporando empresas de bajo volatilidad podemos disminuir el riesgo.
La forma que tiene Buffet de reducir el riesgo es tener una importante porción de liquidez y evitar empresas que coticen a múltiplos altos.
Yo prefiero tener en Cartera algunas empresas de bajo Beta pero está claro que Buffet no puede vender en los momentos de pánico de mercado.
Buffet obtiene una rentabilidad inferior al mercado durante mercados alcistas pero también el riesgo es mucho menor. La cobertura del riesgo se comprueba en los mercados bajistas. .-)

