El otro día salió el tema de las opciones binarias en uno de mis posts, y me puse a indagar cómo está el tema ahora, después de varios años de explosión de este tipo de herramientas. Antes de los números, explico brevemente qué son y luego hacemos las cuentas muy sencillas e interesantes para saber contra qué luchamos.
Opciones binarias
En finanzas existen muchos instrumentos derivados (opciones y futuros) que requieren de unos conocimientos técnicos que la mayoría desconoce (incluso dentro del sector). Con el desarrollo de internet y el mundo de las apuestas online, han proliferado como setas las casas de "apuestas binarias". Porque en efecto, esta operativa forma parte del mundo de las apuestas, no del mundo de las finanzas, aunque a muchos les vendan lo contrario.
Una opción binaria es fácil de entender para cualquiera: es blanco ó negro, es decir, cara ó cruz. En el casino puedes apostar a rojo ó negro, pero si sale el 0 entonces pierdes. Ese es el beneficio de la casa, y el "pequeño detalle" que hace que sea un juego de Esperanza Matemática (EM) negativa para los jugadores.
En el mundo de las Binarias, la casa se reserva su parte de beneficio de otra manera: si aciertas, sólo te llevas el 80% de lo apostado, pero si fallas, pierdes el 100% de lo apostado. Hay cierta variedad de apuestas que se pueden realizar, pero para el ejemplo explicativo me voy a centrar en la más fácil: apostar a que el IBEX (por ejemplo), estará dentro de 15 minutos (ó 5, 60, un día...) por encima ó por debajo del nivel actual. Tan sencillo como eso.
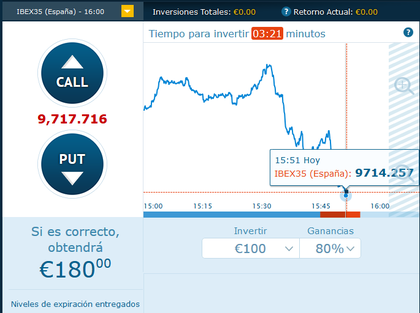
En este ejemplo, voy a apostar 100€. Si dentro de 3 minutos y 21 segundos el Ibex está por encima de los 9714 puntos, entonces ganaré 80€. En caso contrario, pierdo 100€. La cantidad en juego nos dice claramente cuál es el enfoque de estas opciones binarias: estamos en el casino, no en la bolsa. No invertimos, ni siquiera especulamos, estamos jugando... ¿ó no? Porque esto no es exactamente igual que el casino.
La diferencia es que en el casino no podemos hacer nada por modificar la probabilidad de éxito: el rojo y el negro están equilibrados al 50% (en teoría). En cambio en bolsa, aunque la media de los jugadores es del 50%, nosotros podemos elegir el activo, el horizonte temporal y el momento en el que realizar esa apuesta. Si somos capaces de encontrar puntos de entrada con una probabilidad de éxito (fiable) del 60%, ¡ podemos ganar dinero !
Probabilidad y Esperanza Matemática (EM)
Voy a explicar a continuación unos conceptos aplicados a las binarias que en realidad son válidos para todo el universo inversor, sea cual sea tu método y horizonte de inversión. Es el a-c-b de la matemática financiera que todo inversor / especulador debe comprender y manejar con gran soltura.
EM del juego de cara y cruz
Lanzando una moneda al aire, tenemos un 50% de probabilidad de fallo y éxito. Si ganamos 100€ si sale cara y perdemos 100€ si sale cruz, a la larga estamos ante un juego de EM = 0. Es decir, nos resulta indiferente (económicamente) jugar ó no jugar. Pero, ¿qué pasa si ganamos 110€ si sale cara y perdemos 100€ si sale cruz? Entonces la EM es positiva, pero ¿cuánto? Vamos a poner números y explicar la fórmula clave.
El término EM (Esperanza Matemática) es un poco técnico. En realidad, a pie de calle diríamos que es la "media de lo que esperamos ganar repitiendo el juego muchas veces". Dicho de otra manera, la EM es en realidad una media. ¿Cómo se calcula? Simplemente multiplicando la probabilidad de cada suceso por la recompensa (ó castigo) de cada suceso.
EM = (50% * 110 ) + (50% * -100)
Al poner ciencuenta por cien (50%) hablamos de un porcentaje, que en la fórmula se expresa como 0,50.
Es decir, 50% = 50 / 100 = 0,50
Por otra parte, cuando el suceso es "perdemos 100€" entonces le pongo un "menos" delante, es decir, va restando.
Multiplicar una cantidad por 0,50 es igual a multiplicar esa cantidad por un medio (1/2), es decir, coger la mitad.
De tal forma que la fórmula es:
EM = (0,50 * 110) + (0,50 * -100) = 55 + (-50) = 55 - 50 = 5€
Jugar a cara ó cruz con un precio de 110€ si sale cara y una pérdida de 100€ si sale cruz equivale matemáticamente a recibir 5€ (y no lanzar las monedas al aire) cada vez que se plantee una tirada. Dicho de otra manera, podemos esperar ganar 5€ de media en cada tirada.
Este concepto se puede aplicar al mundo del trading y la inversión, ya sea con números exactos ó como concepto a tener siempre en mente cuando vamos a iniciar una operación: ¿cuánto podemos ganar si nuestro análisis es correcto? ¿Cuánto podemos perder si nos equivocamos? ¿Qué grado de fiabilidad tenemos sobre la operación, y por tanto qué probabilidad de fallo creemos que podemos tener?
EM con opciones binarias
En el mundo de las binarias el premio suele ser del 70% ó del 80% de lo apostado. Si apostamos 100€, ganamos 80€ si acertamos y perdemos los 100€ si nos equivocamos.
Si nuestra probabilidad de éxito fuera del 50%, entonces nuestra EM sería:
EM = (0,50 * 80) - (0,50 * 100) = -10€
Si nuestro análisis no aporta valor (a la larga) y viene a ser lo mismo que lanzar una moneda al aire (50/50), entonces si apostamos 100€ como apuesta base, nos da lo mismo apostar que darle 10€ al bróker directamente.
Por lo tanto, lo que nos interesa es calcular cuál sería la probabilidad de éxito mínima que necesitamos tener para operar a muy (pero que muy) corto plazo con este tipo de instrumentos y ganar.
EM = (q * 80) + ( (1-q) * -100)
donde q = probabilidad de éxito
Pongamos una probabilidad de éxito igual a q=55%, entonces la probabilidad de fallo es del 45%, es decir, 100% - 55%, ya que por definición, la probabilidad de acertar más la probabilidad de fallar es igual al 100%.
De ahí que la probabilidad de fallo se escriba como : (1-q)
Recuerden que la probabilidad es escribe en "tantos por uno" en vez de en "tantos por cien", lo cual significa que si la probabilidad de éxito es del 55%, entonces q=0,55 y (1-q)=0,45.
Nuestra fórmula si q=55% sería:
EM = (0,55 * 80) + ( 0,45 * -100) = 44 - 45 = -1€
La EM es por tanto negativa con una probabilidad del 55%, necesitamos más, pero no mucho más. Cada vez que hagamos esta operación, sabemos que perderemos 1€ de media. Como la ganancia ó pérdida son fijas, tenemos que fijarnos en la probabilidad de éxito. ¿Qué tasa de acierto ó probabilidad de éxito tenemos que tener para que este juego nos resulte rentable y valga la pena jugarlo?
Pues tenemos que despejar la "q" en la fórmula de arriba, de forma que EM = 0. Vamos paso por paso:
0 = (q* 80) + ( (1-q) * -100)
0 = 80q - ( 100 * (1-q) )
0 = 80q - ( 100 - 100q)
pasamos el segundo término a la izquierda, y pasa de restar a sumar:
100 - 100q = 80q
100 = 180q
y finalmente:
q = 100 / 180 = 55,56%
El punto de equilibrio donde la EM es nula es por tanto una probabilidad de éxito del 55,56%. Si somos capaces de obtener una probabilidad superior, merece la pena jugar a este juego. En caso contrario, es un juego perdedor para nosotros.
Globalmente, a muy corto plazo (muy intradía), los movimientos del mercado son erráticos y aleatorios, al menos durante la mayor parte del tiempo. O al menos, visto globalmente, la masa de los traders tienen una probabilidad de acierto del 50%, y eso es justamente lo que explotan los "brokers binarios", ofreciéndonos un juego que si fuera de cara ó cruz, con una probabilidad del 50%, sería claramente perdedor para nosotros.
EM y el casino
Por compararlo con el casino, y fijar así conceptos de probabilidad, vamos a ver si este juego de las opciones binarias exige más o menos probabilidad de acierto que la ruleta de los casinos.
Como saben, la ruleta tiene 36 números, 18 negros y 18 rojos, y además tiene el "cero", donde sólo gana la casa.
La probabilidad que tiene la casa de ganar es por tanto de: q = 1 / 37 = 2,7%
Nosotros como apostantes tenemos:
probabilidad de que salga el rojo ó el negro (es la misma): q = 18 / 37 = 48,65%
Esa es la clave de la ruleta. Es como el juego de cara y cruz pero con una probabilidad trucada que se rebaja del 50% al 48,65%. Si el premio y castigo son iguales, por ejemplo 100€, es fácil deducir que la EM es negativa.
Veamos cuánto:
EM = (0,4865 * 100) + ( (1 - 0,4865) * 100) = 48,65 - 51,35 = -2,70€
¡ Qué sorpresa ! Nuestra EM es justo lo que gana la banca (porque he puesto 100€ de apuesta base). A comparar con la EM de -10€ que vimos en las opciones binarias, nos hacemos idea del margen que tienen los brokers binarios, para cubrirse de errores y fluctuaciones, muy superior al casino (donde en cambio no tenemos margen alguno para modificar esa probabilidad de éxito a nuestro favor). Cada cual que juzgue.

