En mi último artículo (que por cierto todavía no he tenido
tiempo de copiar a INBESTIA) disponible aquí: http://www.ferrerinvest.com/14/post/2012/11/el-efecto-mariposa.html
comentábamos como se hacía para dar un parte meteorológico. En dicho artículo,
hubo un comentario del usuario Toni que me preguntaba lo siguiente:
Entonces, ¿crees que
sería posible predecir con bastante acierto la dirección en bolsa de los
valores e índices?.
Voy a intentar darle una respuesta un poco más amplia en
este POST y de paso vamos a ver un ejemplo práctico de la utilización del
teorema de Bayes a la bolsa.
No se si “predecir” es la palabra correcta en este caso,
pero si que es posible estimar con bastante acierto las probabilidades de que
un índice o una acción suba utilizando el teorema de Bayes.
Para ello he utilizado dos instrumentos que a todos nos son
claramente familiares y se ha hablado muchas veces en múltiples POST sobre su
correlación y funcionamiento: El VIX y el S&P 500.
Generalmente se utiliza el S&P 500 y no el IBEX porque
el VIX está calculado utilizando las opciones sobre este índice. Es como
trabajar con un estándar, pero podéis aplicar el contenido de este artículo a
cualquier variable o índice incluido los datos de los balances de cuenta.
El VIX es el índice del miedo, como le gusta llamarle Hugo.
Si el VIX sube o está muy alto pronostica altas volatilidades y caídas en los
mercados (generalmente). ¿Hasta qué punto esto es cierto?
Para hacer el análisis en primer lugar, nos vamos a yahoo
finance y nos descargamos los datos de ambos instrumentos desde 1990:
http://finance.yahoo.com/q/hp?s=%5EGSPC&a=00&b=3&c=1990&d=10&e=26&f=2012&g=d
http://finance.yahoo.com/q/hp?s=%5EVIX+Historical+Prices
Acto seguido utilizamos el EXCEL para aplicar la fórmula de
Bayes. Hay una descripción de cómo utilizar dicha fórmula por si os perdéis en
la Wikipedia:
http://es.wikipedia.org/wiki/Teorema_de_Bayes

No os asustéis aunque veáis muchas letras raras! Solo es
necesario saber sumar, restar, multiplicar y dividir, como más adelante veréis,
para aplicar este teorema y tener un modelo matemático cuantitativo para
nosotros.
Lo primero que hemos hecho ha sido coger el EXCEL y
descargar el histórico de precios. En la última columna después del último
precio, ponemos un 1 si el instrumento ha subido y un 0 si ha bajado. Así
podemos contar el número de días que sube el SP500 o el VIX en dos hojas
diferentes.
Es necesario calcular
lo siguiente:
- El número de veces que el VIX sube y el SP también sube.
- El número de veces que el VIX baja y el SP también baja.
- El número de veces que el VIX sube y el SP baja.
- El número de veces que el VIX baja y el SP sube.
Una vez calculado, pues creamos una tabla como la siguiente:
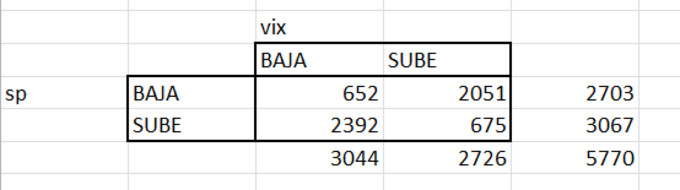
Los números que hay a la derecha es la suma de los de la
izquierda, 2703= 652 + 2051. 5770 = 2726+3044. El resto es igual es la suma,
5770 es el número total de días analizados.
Ahora viene lo divertido, queremos calcular:
¿Cuál es la probabilidad de que el
índice S&P 500 baje si el VIX sube?
Para calcular esto vamos a aplicar la fórmula de Bayes,
disponible en Wikipedia que es la siguiente:

Para ello debemos calcular:
- P(II) = Probabilidad de que el índice incremente su valor
- P(ID) = Probabilidad de que el índice decrezca en valor.
- P(VD) = Probabilidad de que el VIX decrezca en valor.
- P(VI) = Probabilidad de que el VIX incremente su valor.
Y la ecuación quedaría de la siguiente forma:
P(ID|VI) =
P(ID)* P(VI|ID) / P(VI)
- La probabilidad de que el índice S&P 500 baje es P(ID) =
2703/5770
- La probabilidad de que el VIX incremente si el índice S&P
Baja es P(VI | ID) = 2051/2703
- La probabilidad de que el VIX incremente su valor es P(VI) =
2726/5770
Pues hay un 75,23% de probabilidades de que P(ID | VI) el
índice decremente de valor cuando el VIX incrementa su valor.
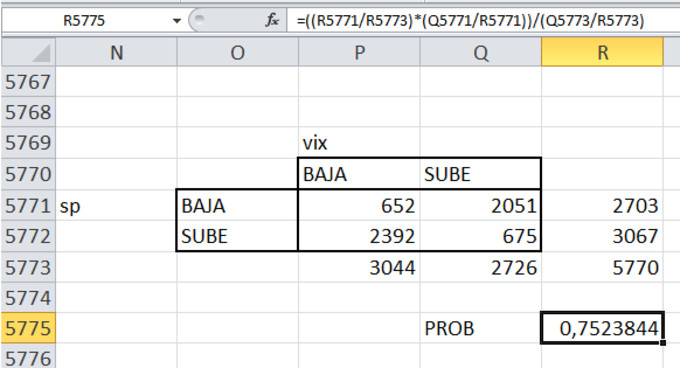
Todos estos cálculos están realizados basándose en el mismo
dia, el mismo dia que el S&P sube comprobamos que el VIX suba. Pero podemos
hacer los cálculos sobre lo que pasó en una semana después por ejemplo y
verificar correlaciones.
Además, como podéis ver todos estos datos se van
realimentando, a medida que tenemos más histórico las probabilidades van
cambiando y esto puede acabar desarrollándose en un algoritmo adaptativo para
seguir la tendencia de los valores/índices.
Esto solo es un ejemplo entre el VIX y el S&P. Dos
variables muy sencillo, se le pueden añadir más variables, por ejemplo añadir
la curva de tipos, los datos de los balances o ratios como el PER, etc. Con esto podemos crear
nuestro propio modelo matemático igual que los que utilizan los hedge funds,
teniendo en cuenta, eso sí, que siempre va a haber más de un 24% de
probabilidades de que el S&P termine subiendo aunque el VIX suba.
Existen multitud de aplicaciones como veis, creación de
indicadores, búsqueda por fuerza bruta de correlaciones haciendo todas las
combinaciones de instrumentos posibles…
Muy buen post Mario!
Creo qeu una de las claves para sacarle tajada al mercado es usar patrones y relaciones que funcionen estadísticamente a lo largo del tiempo.
Un saludo!
Muy buen post Mario!
Creo qeu una de las claves para sacarle tajada al mercado es usar patrones y relaciones que funcionen estadísticamente a lo largo del tiempo.
Un saludo!
Hola Mario,
En primer lugar agradecerte este interesante post sobre técnicas cuantitativas.
Quería comentarte que, de la manera que realizas los cálculos de la tabla (aplicando la regla de Laplace), el Teorema de Bayes es redundante. Podrías obtener el mísmo resultado, siguiendo tu razonamiento, dividiendo los casos favorables (2051) entre los casos posibles (2726), como haces para los otros términos.
Más allá, pienso que sería más conveniente calcular el coeficiente de Pearson para determinar la correlación entre ambos índices (que, en éste caso, sería inversa). Aplicando, a continuación, un test de Student se podrían obtener conclusiones sobre la significación probabilísticas.
Gracias de nuevo por el post y un saludo,
Alvaro
Hola Alvaro!
Gracias por el comentario! Tengo qreconocer que las matematicas no son mi fuerte precisamente, pero de vez en cuando como mero divertimento esta bien hacer cosas con ellas.
Saludos,
Hola de nuevo,
He estado leyendo la wikipedia respecto a la tstudent y la siguiente pagina:
http://www.conexionismo.com/leer_articulo.php?ref=prueba_t_de_student_para_dos_muestras_relacionadas-902ybsd7
El coef de pearson lo utilizamos para saber como estan correlacionadas las dos poblaciones y luego nos aseguramos que realmente haya correlacion utilizando la prueba de tstudent. Habia realizado algo parecido algo parecido cuando hacia test de cointegracion con el test de dickey fuller aumentado. La pregunta es, una vez que ya tenemos eso como lo utilizamos para especular de forma mas o menos utiles?
Yo lo hacia con desviaciones estandar, poniendome a largos en uno y a cortos en otro. Recuerdo que tal vez era alli donde fallaba, como podemos representar graficamente el spread para ver si se desvia de la media x desviaciones estandar?
Gracias una vez mas por el comentario.
Hola Mario, acabo de ver tu comentario sobre el ADF y tu pregunta sobre el modelado del spread para pairs trading (parece que no me ha funcionado la notificación automática...)
A ver: existen varias maneras de modelar el spread. Algunas de ellas es aplicando modelos autorregresivos, pero requieren parametrizar el modelo (órdenes, etc), lo cual puede ser complejo de implemetar. El modelo que yo prefiero es uno no paramétrico en el cual, básicamente, se procede a la aplicación de una regresión lineal entre ambas series para determinar Gamma (coeficiente de cointegración) y Nu (media). Posteriormente se aplicaría el ADF al spread resultante para verificar si es estacionario. Esto se llama el método de dos pasos de Engle-Granger:
http://en.wikipedia.org/wiki/Cointegration#The_Engle-Granger_two-step_method
Una vez verificada la estacionariedad, como bien señalas, podrías ir largo o corto al spread mediante la compra de un valor del par y la venta del otro, pero en las proporciones indicadas por Gamma (no uno a uno).
Bueno, espero que te haya aclarado algo.
Un saludo,
Alvaro
Hola alvaro,
Acabo de ver el comentario. Me leo el enlace y te comento. Feliz navidad!
Como sugerencia, en vez de tener en cuenta únicamente si el VIX sube o baja, ¿no podríamos valorar como subida o bajada sólo a partir de un movimiento mayor a "x"?
Es decir, no tiene el mismo significado una subida pequeña en comparación a una mayor. De modo que así podría aumentar la probabilidad estadística.
Este teorema lo utilizamos a diario como valores predictivos en Medicina, y hablamos de rangos de valores para aumentar la eficacia predictiva. Lo que viene a ser la diferencia entre sensibilidad/especificidad.
Hola Jose,
Lo del vix era un ejemplo. No entiendo a que te refieres con lo de los rangos de valores, necesito un ejemplo xa comprenderlo.
Ssludos
Hola,
Si lo he entendido bien, evalua la correlación entre el VIX y el S&P 500 observando que la mayoría de las veces que el VIX baja, el S&P 500 sube y viceversa.
¿No podríamos utilizar más variables con respecto al VIX que únicamente si sube y baja (sin meternos en añadir otras como el PER) como por ejemplo, el contexto respecto a su media de 20 y su significación estadística?
Por eso hablo de establecer un rango de valores, es decir, no es lo mismo una subida de medio punto que una de un punto entero, ni es el mismo contexto una subida en 21 que una subida rondando los 38. Y sin embargo, ambas serían una subida.
Sólo comentaba si es posible contextualizar un poco esos 1 o 0 de subida o bajada.
Saludos.

