La Antimartingala

El presente artículo pretende explicar una gestión monetaria alternativa que podría ser interesante en ciertos sistemas de trading.

La Martingala es una forma de apostar, donde aplicado al trading, supone realizar una gestión monetaria en la que se va aumentando el tamaño de la posición a medida que vamos perdiendo, con la idea de recuperar en la primera operación ganadora todo lo perdido anteriormente más la cantidad arriesgada en nuestra primera operación.

Todo aquel que lleve un tiempo en los mercados sabe que esta técnica puede arrojar unos resultados sorprendentes. El problema es que en este caso las matemáticas juegan en nuestra contra, y un número de pérdidas seguidas no tan elevado puede comprometer seriamente la supervivencia de nuestra cuenta.

Lo que se plantea en este artículo es precisamente lo contrario. Es decir, en lugar de ir doblando el tamaño de nuestra posición una vez tengamos una pérdida, lo doblaremos en caso de obtener una ganancia, algo que podría llamarse Antimartingala, pues aumentamos el riesgo al ganar y no al perder.

La idea que subyace detrás de esta técnica es que en algún momento se producirá una racha de operaciones ganadoras que permitirá compensar todas las operaciones perdidas anteriormente y ganar mucho más.

Viendo esto con un ejemplo rápido, si tenemos 7 operaciones ganadoras consecutivas, podremos compensar 127 operaciones perdedoras (1+2+4+8+16+32+64), por lo que si esta racha se produce antes de las 127 operaciones, nuestra cuenta estará en positivo.

Si bien luego realizaremos diferentes matizaciones, esta idea se puede ver gráficamente como sigue, en un ejemplo donde “reseteamos” tras obtener una racha de 7 operaciones consecutivas ganadoras:

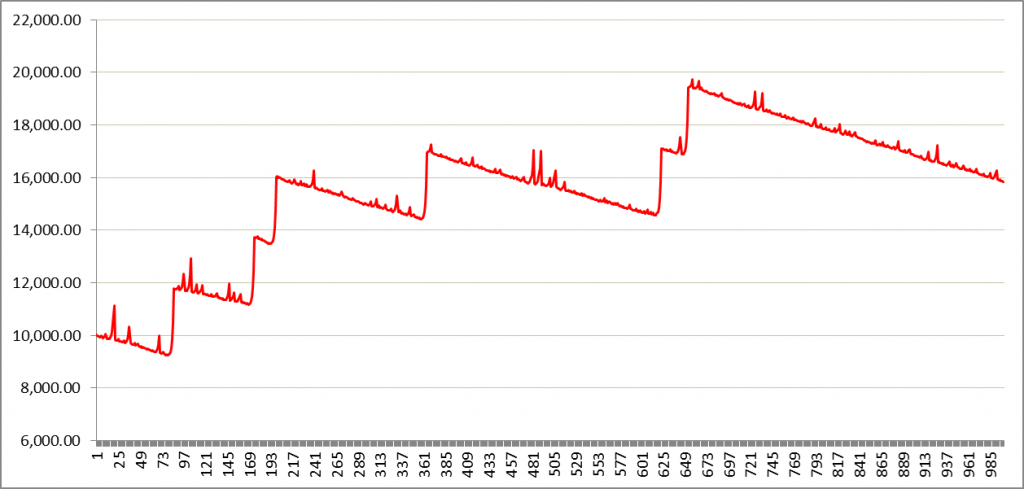
Es decir, la curva de balance tenderá a bajar hasta que se produce una racha de operaciones ganadoras, momento en el cual el balance de la cuenta experimenta un salto vertical.

Antes, un poco de Estadística

Como podréis imaginar, esta técnica requiere “resetear” en algún momento el proceso de ir doblando el número de lotes, puesto que al final, tarde o temprano acabará llegando una pérdida y por tanto este sistema nunca podría ser ganador si realizamos ese proceso de manera indefinida.

En la calculadora que incluiremos a continuación se han hecho simulaciones con 5, 7 y 9 operaciones ganadoras seguidas para ver cómo evoluciona la curva en cada uno de esos supuestos.

Con todo, antes de todo deberíamos ver algo de estadística básica. Hay una fórmula muy sencilla para ver la probabilidad que tenemos de encadenar una serie de operaciones ganadoras o perdedoras. En concreto:

Racha de Pérdidas Teórica = (% fallos) ^{nº pérdidas consecutivas}

Racha de Ganancias Teórica = (% aciertos) ^{nº ganancias consecutivas}

Por ejemplo, si tenemos un sistema con un porcentaje de aciertos del 60% y queremos saber la probabilidad de concatenar 7 operaciones ganadoras, utilizaremos la siguiente fórmula.

60% ⁷ = 2,7994%

Por lo tanto, si tenemos en cuenta que 1/2,7994% = 36, quiere decir que en promedio, necesitaremos 36 operaciones para obtener 7 ganancias consecutivas.

En base a esta fórmula, podremos por tanto construirnos una tabla donde se indica el número de operaciones de media en la que podemos esperar aparezca una racha de operaciones ganadoras en base al porcentaje de aciertos de nuestro sistema.

Es decir, con un sistema que arroje un porcentaje de aciertos del 65%, necesitaremos en media 48 operaciones para tener una racha de 9 operaciones ganadoras, recuperando tras la misma un total de 511 operaciones perdedoras (1+2+4+8+16+32+64+128+256).

Calculadora en Excel

Se adjunta una calculadora en Excel que nos permitirá simular los resultados que podríamos obtener aplicando una gestión monetaria Antimartingala, si bien antes pasaremos a explicar un poco los parámetros a definir por el usuario.

• *  Balance Inicial: Como su nombre indica, muestra el saldo de nuestra cuenta de trading al inicio.
• *  Lotes Iniciales: Indica los lotes con los que partimos en la simulación. En este ejemplo, 0,02 lotes o 2.000 unidades de la divisa base (2.000 EUR en el caso del EURUSD)
• *  Riesgo por Lote: Indica lo que arriesgamos en cada operación por cada lote completo. Es decir, si tenemos un riesgo por lote de 1.000 unidades monetaria y empezamos con 0,02 lotes, quiere decir que nuestra operación arrojará un resultado de 20 unidades monetarias (0,02 * 1.000 unidades).
• De esta forma, podremos ajustar ambos parámetros para replicar nuestra operativa habitual. Por ejemplo, si normalmente operamos con 80 pipos de SL, pondremos que el riesgo por lote son 800 (100.000 * 0,0080), y luego ajustaremos el tamaño de los lotes iniciales para adecuar el riesgo al tamaño de nuestra cuenta.
• En este caso señalar que sería mejor simular el balance de una cuenta en divisa secundaria (por ejemplo, el USD en el caso de operar EURUSD), puesto que de esta manera el valor de 1 pipo se mantiene constante (en EURUSD el valor de 1 pipo en USD siempre es 10USD, mientras que el valor de 1 pipo en EUR irá variando en base a cómo esté el tipo de cambio EURUSD).

• *  Operaciones: Indica el número de operaciones a realizar, estando la hoja limitada a 1.000 operaciones en este caso. Cualquiera con unas nociones básicas de Excel podrá ampliar el número. Por supuesto, se puede simular el resultado de 300 o 500 operaciones.
• *  Porcentaje de Aciertos: Indicar el porcentaje de aciertos que arroja nuestro sistema de trading
• *  Ratio Riesgo / Beneficio: Indicar el ratio de las ganancias respecto a las pérdidas. Es decir, cuánto ganamos respecto a lo que perdemos. Si ponemos como en el ejemplo un ratio de 1.20, quiere decir que cuando ganamos lo hacemos en 1.2 unidades, y cuando perdemos lo hacemos en 1 unidad.
• *  Gestión Monetaria: Viene a indicar en qué porcentaje queremos aumentar el tamaño de la posición a media que aumenta el balance.

En las columnas O, Q y S se realiza un ratio del balance actual respecto al balance inicial, y básicamente lo que se hace es calcular el exceso y multiplicar el mismo por el porcentaje de gestión monetaria señalado según la siguiente fórmula

Lotes = Lotes iniciales * ( 1 + (Ratio balance – 1) * % Gestión Monetaria)

Si este porcentaje está al 0%, no realizará gestión monetaria alguna, y si está al 100%, la realizará en su totalidad, siempre ajustando a 2 decimales puesto que asumimos no podemos contratar menos de 0,01 lotes.

Por ejemplo, este sería el resultado de la fórmula en base al porcentaje de gestión monetaria señalado partiendo de 0,10 lotes

• *  Riesgo intereses compuestos: Hemos realizado una simulación adicional asumiendo una gestión monetaria tradicional, donde se arriesga un X% por operación, de forma que podremos comparar los resultados de balance con un sistema muy extendido respecto al sistema Antimartingala.
• *  Comentar por último que las celdas D9, G9 y J9 son configurables para poder simular rachas diferentes a las expuestas en este ejemplo (5, 7 y 9), por lo que podrás probar con otros números.

Sin más, dejo una copia de la calculadora en Excel para su descarga

Aplicando Montecarlo

Si le has dedicado algo de tiempo a la hoja realizando diferentes simulaciones con la tecla F9, verás que los resultados en cada prueba pueden variar enormemente. Esto es así porque el resultado final dependerá totalmente del número de rachas y momento en que éstas se producen, por lo que para tener un resultado estadístico fiable de lo que podemos esperar en promedio de una gestión de este tipo tenemos que recurrir a la simulación de Montecarlo.

Básicamente, por resumirlo de una manera comprensible, lo que haremos será calcular muchas veces cual es el resultado de aplicar esta metodología. En lugar de darle a F9 (calcular) durante N veces y apuntar el resultado, dejaremos que Excel lo haga por nosotros, aplicando una media a las 500 simulaciones realizadas.

De esta manera, tendremos una aproximación mucho más realista de lo que esperar con esta metodología.

En la pestaña “Montecarlo” tenéis los resultados del balance final y las rachas de operaciones consecutivas para 500 iteracciones. La manera de realizar esto es muy sencilla, pues para ello utilizamos la función “Tabla” (“Table” si utilizas Excel en inglés) y señalamos una celda vacía en uno de sus argumentos.

Excel lo que hará entonces será recalcular toda la hoja para cada una de las 500 iteracciones, mostrando el resultado en cada una de las filas. Posteriormente hacemos una media de cada una de las columnas (Celdas C4:I4 de la pestaña Montecarlo) y ya tenemos el resultado final.

Consideraciones

En primer lugar, señalar que la comparación de esta técnica Antimartingala respecto a una gestión monetaria tradicional (arriesgar un % fijo por operación) va a depender en gran medida de los lotes iniciales con los que partamos en una gestión Antimartingala.

Hay que tener en cuenta que lo normal sería encadenar un número bastante elevado de pérdidas antes de ver una racha ganadora, por lo que el riesgo de partida deberá ser muy inferior al de la gestión tradicional.

En segundo lugar, indicar que los resultados que arroja Montecarlo no dejan de ser una media, pero si nos fijamos en el máximo y el mínimo de las columnas de balance de la hoja de Montecarlo, veremos que la dispersión es enorme, y encontramos resultados donde la rentabilidad prácticamente es nula, a resultados donde la rentabilidad tiene 3 o 4 dígitos.

En tercer lugar, indicar que los resultados mejoran exponencialmente a medida que nuestro sistema arroja un porcentaje de operaciones ganadoras mayor. Es decir, la diferencia entre un sistema que gane un 52% de los casos respecto a otro que gane un 58% de los casos es abismal en cuanto al resultado final.

Por último, indicar que esta técnica conlleva unos efectos psicológicos seguramente difíciles de llevar por una persona. Si bien esos efectos se diluyen cuanto menor sea el número de operaciones ganadoras que hayamos establecido antes de “resetear” el tema, vamos a tener muchas operaciones perdedoras consecutivas, algo difícil de llevar.

Conclusiones

Realmente no conozco a nadie que aplique una técnica de gestión monetaria como la explicada en este artículo, pero debo reconocer que los resultados obtenidos han llamado mi atención. Dicho esto, creo que realmente esto es más un ejercicio teórico que algo que realmente pueda llevarse a la práctica.

Dicho lo anterior, una gestión de este tipo podría ser factible en sistemas con un alto porcentaje de aciertos, pues el número de rachas ganadoras será bastante alto en consecuencia, y el resultado muy positivo a pesar de que el ratio beneficio / riesgo seguramente sea bastante menor a 1.

Como siempre en cualquier artículo, abro un hilo en el foro para comentar sobre el mismo. No dejéis de comentar vuestras conclusiones en caso de que profundicéis en este tipo de gestión alternativa.

Foro: Artículo Antimartingala – Dudas o Comentarios

Y por supuesto, estaré encantado de resolver cualquier duda que podáis tener respecto al Excel adjunto en este artículo.

Anexo: Calculadora Racha Teóricas Montecarlo

He querido dejar otra calculadora en Excel para comprobar que efectivamente la fórmula que calcula el número en promedio que necesitamos para tener una racha de operaciones ganadora funciona correctamente, y para ello, lo que he hecho ha sido realizar una simulación en Excel de estos números.

Antes de nada, te puedes descargar la calculadora en desde aquí:

El funcionamiento de esta calculadora es realmente sencillo, pero por si acaso, paso a explicar cómo se ha construido a continuación:

• *  Indicamos en la celda D5 el porcentaje de aciertos que queremos simular
• *  Indicamos en la celda D5 el número de operaciones que queremos simular
• *  La columna B indica el número de operación (hasta 10.000)
• *  La columna C nos genera un número aleatorio donde pondrá un 1 si la operación es ganadora, y un 0 si es perdedora. El porcentaje de operaciones ganadoras se puede observar en la celda C10, que deberá aproximarse al valor puesto en la celda D4.
• *  En la columna D hacemos un conteo de las operaciones ganadoras consecutivas
• *  En la columna E contamos la racha que se ha producido. Es decir, será el máximo valor alcanzado por la columna D hasta que se pierde una operación.

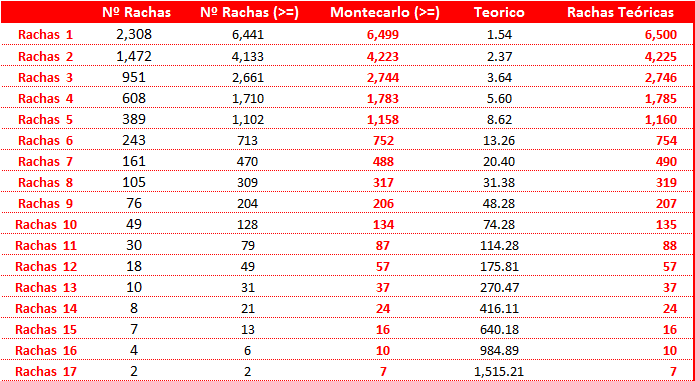
El cuadro resultante en las columnas G:L viene comentado en la propia hoja Excel. Básicamente, lo que hacemos es contar el número de rachas que se ha producido en la simulación, y lo comparamos con el valor teórico que nos sale de aplicar la fórmula antes expuesta:

Racha de Ganancias Teórica = (% aciertos) ^{nº ganancias consecutivas}

Esa fórmula nos proporciona el número de operaciones que necesitamos para tener una racha, por lo que sabiendo el número de operaciones que estamos simulando (D5), podemos sacar sin problema alguno el número de rachas teóricas que tenemos que obtener (columna L).

La diferencia entre las columnas “I” y “J” es que la columna “I” es el resultado de una simulación, mientras que la columna “J” es la media de 1.000 simulaciones que se han realizado por Montecarlo en las columnas N:BB.

Como se puede apreciar, si comparamos las columnas “Montecarlo (>=)” y “Rachas Teóricas”, estas coinciden casi milimétricamente, demostrando cómo se puede hacer una aproximación a través de Montecarlo en Excel, y cómo la fórmula antes expuesta se cumple en una simulación.