En el post anterior de esta serie sobre la independencia financiera, estuvimos viendo cuánto se puede ganar invirtiendo en bolsa, y fijamos un techo matemático en torno al 30-40% anual, y un techo empírico en torno al 20% de media anual a largo plazo. Alguno se preguntará, ¿entonces, si no se pueden dar pelotazos año tras año, cómo se puede hacer uno rico invirtiendo? Salvo que dispongas de un capital inicial elevado, ó de una elevada capacidad de ahorro mensual, será difícil... ¿ó no?
Dado que los términos frío/calor, fácil/difícil, etc, son subjetivos y significan cosas distintas para unos y otros, vamos a poner números concretos y cuantificar cómo de fácil ó difícil es alcanzar un capital de "independencia financiera". Para ello, lo primero que es necesario explicar, y es el objetivo de este post, es la Ley de Capitalización Compuesta (LCC) y todo lo que implica. Es decir, no sólo basta con saber qué es; necesitamos jugar con ella hasta haberla asimilado en profundidad. Porque es uno de los secretos de los que ganan en bolsa a largo plazo.
Hay muchas cosas en la vida que a priori parecen difíciles pero a posteriori resultan simples y fáciles. ¿Será la libertad financiera una de ellas? Mi opinión es que sí.
¿Qué es la libertad e independencia financiera?
En otros países se le llama "ser rentista", porque no tiene esa connotación negativa que tiene aquí. Pero poco importa: la idea es alcanzar un patrimonio que bien gestionado nos permita liberarnos de la obligación de generar un sueldo mensual a través del trabajo. Ese objetivo adquiere una importancia extraordinaria para la gente que tiene un trabajo que no le gusta. ¿Es algo utópico e irreal ó hablamos de algo razonable y lógico? Vamos a verlo con datos.
Como ocurre muchas veces que queremos transmitir una idea importante, nos tenemos que enfrentar primero a una serie de prejuicios y de aprendizajes erróneos sobre los que se sustenta la creencia equivocada. No podemos enseñar a hacer integrales a gente que no ha aprendido bien a multiplicar y hacer derivadas.
Por eso, vamos a empezar por explicar y describir en este post, qué es y qué impacto tiene la Ley del crecimiento exponencial, y en próximos artículos hablaré del doble enfoque necesario:
1- la parte filosófica de la vida, que todos debemos comprender bien si queremos alcanzar la libertad financiera, y
2- la parte técnica de la inversión a largo plazo (rentabilidades esperadas, formas de controlar el riesgo, etc) que trata de conceptos extremadamente sencillos, que los grandes inversores conocen en profundidad, y que todo el mundo puede comprender con un poco de "reprogramación mental".
La ley exponencial: el punto en común de todos los gurús de las finanzas
Cualquier método ganador de inversión (técnico, value, macro etc) explota las propiedades matemáticas de la capitalización compuesta. Muchos han oído hablar de ella, y creen que saben en qué consiste. Pero hay que asegurarse de que hemos captado toda la esencia y la potencia de esta Ley de la naturaleza que también se aplica a las finanzas. Para ello vamos a definirlo brevemente, y después vamos a hacer números con ejemplos reales.
Definición.
En matemática financiera, hay dos leyes de capitalización:
- La ley de capitalización simple: los beneficios obtenidos cada año (los intereses por ejemplo), se quitan de la cuenta (para gastarlos), y el año siguiente empieza con el mismo capital inicial.
La capitalización simple consiste en que cada año hacemos:
capital final = capital inicial * (1+i)
donde i=tipo de interés anual.
- La ley de capitalización compuesta (LCC): los beneficios obtenidos cada año se dejan en la cuenta, y se reinvierten con el resto del capital. Por tanto, cada año vamos haciendo crecer la "bola de nieve".
En la ley de capitalización compuesta (LCC) se reinvierten los beneficios, de tal forma que cada año:
capital final = capital final del año anterior * (1+i)
Y el "capital final del año anterior" es a su vez igual a:
capital final hace 2 años * (1+i)
De aquí resulta que el capital final tras "n" años de inversión es igual a:
capital final tras n años = capital inicial * (1+i)n
La LCC va totalmente en contra de nuestra naturaleza humana, que percibe en esencia sólo lo que es lineal. Nuestra mente no está preparada para captar en su profundidad cualquier manifestación que sea de carácter exponencial, como lo es la LCC. Porque esa es la clave de la LCC: que su crecimiento es exponencial.
En este gráfico vemos la diferencia entre un crecimiento lineal (en rojo) y un crecimiento exponencial (en verde). Durante los primeros años no hay grandes diferencias, pero a partir de los 10 años, la diferencia se nota, y es cada vez mayor. Esa es la gran clave de todo inversor con éxito: su capacidad de focalizarse única y exclusivamente en el largo plazo. Es algo difícil psicológicamente, porque la conexión entre el esfuerzo ó sacrificio y el resultado tarda mucho en verse.
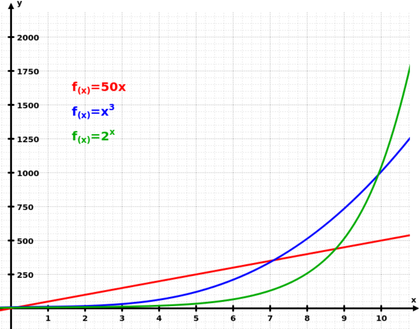
Parece sencillo de comprender, y lo es. Pero donde no terminamos de captar la enormidad de esta propiedad matemática es en sus consecuencias a largo plazo. Cuanto mayor sea ese plazo temporal, más nos cuesta como seres humanos, imaginar y captar la dimensión de lo que va creciendo, ya sea dinero, conejos, plantas, ó células. Todo eso son ejemplos de crecimientos exponenciales en la naturaleza.
Aquí va una adivinanza que se basa en la ley exponencial (como la LCC):
Si un nenúfarduplica su tamaño cada día, y se sabe que al cabo de 32 días ocupa toda la superficie del lago, ¿cuántos días tarda en ocupar la mitad de la superficie del lago?
Veamos algunos ejemplos para testear la capacidad de asimilación de la LCC. El objetivo es responder a estas preguntas de forma intuitiva, es decir, sin hacer ningún cálculo escrito (pero sí mentalmente).
(respuestas al final del artículo).
a. ¿Cuánto dinero obtenemos invirtiendo 100€ hoy dentro de 100 años al 10%?
b. Capital final de 1000€ invertidos hoy al 30% anual dentro de 50 años.
c. Capital final de 1€ invertido al 2% desde que nació Jesucristo (2014 años).
Más ejemplos, entrando en materia de lo que nos interesa: invertimos tan sólo 1000€ hoy a distintos tipos de rentabilidad anual durante 25 años. Nótese que no invertimos nada más, es decir, no añadimos ahorro mensual. Tan sólo 1000€ de capital inicial, y vamos a ver cuánto obtenemos de capital final (dentro de 25 años):
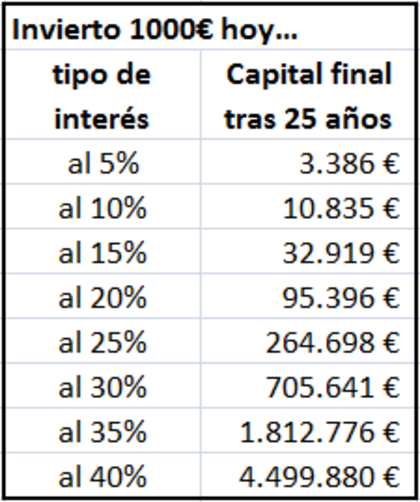
En esta tabla podemos ver (con números) lo que significa la palabra "exponencial". Algunas comparaciones interesantes:
- del 5% al 10%, obtengo el doble de rentabilidad (x2), pero mi capital final se multiplica por 3,2 (y no por 2).
- del 10% al 20%, la rentabilidad también es del doble, pero mi capital final se multiplica por más que 9. Ya empezamos con palabras mayores. Nueve veces más capital final.
- del 20 al 40% vuelvo a duplicar la rentabilidad anual (x2), pero el capital final que obtengo es 47 veces mayor (x47).
- del 5% al 40%, mi rentabilidad anual es ocho veces mayor (x8), pero mi capital final se multiplica por más de mil trescientos (x1328).
Pensemos en las consecuencias de esta tabla. Fíjense en el 40% anual. Estamos diciendo que si alguien es capaz de obtener una rentabilidad (media) anual del 40% durante 25 años, es decir, de forma consistente a largo plazo, conseguirá un capital final de casi 4,5 millones de euros habiendo invertido tan sólo 1000€ al principio. ¿No les parece absolutamente increíble? Una persona de 40 años estaría a tiempo de constituir un fenomenal capital para su jubilación.
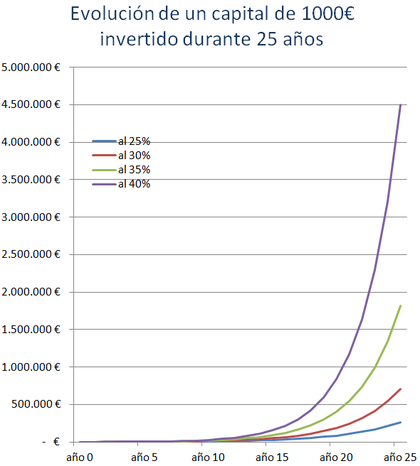
En el siguiente gráfico podemos comparar los capitales finales constituídos en función de la rentabilidad anual que seamos capaces de obtener. Fíjense por ejemplo en el salto que damos entre obtener un 30 y un 40% al año.
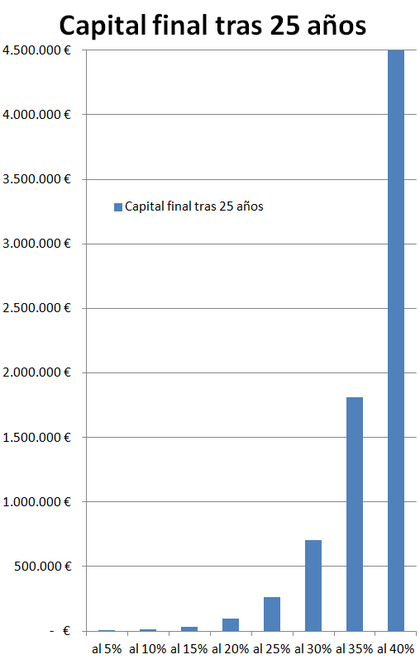
Y ahora vamos a comparar la evolución de nuestro capital a lo largo de esos 25 años, en función de distintas tasas de rentabilidad. Aquí es donde vemos la forma típica de una curva exponencial, cuya pendiente de crecimiento es cada vez mayor (mientras que una curva lineal siempre muestra la misma pendiente de crecimiento).
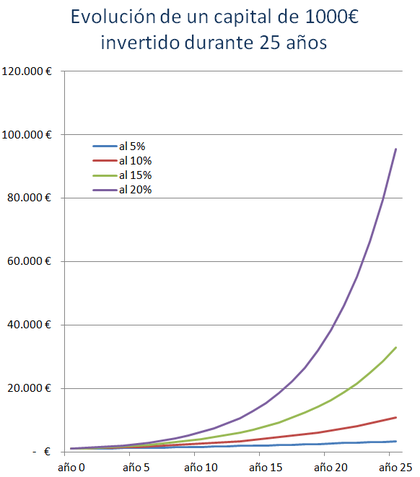
Genios y gurús frente a charlatanes y estafadores.
Los ejemplos anteriores nos muestran el impacto brutal que tiene a largo plazo unos puntos más o menos de rentabilidad anual. ¿Qué pensar de alguien que le promete un 60% de rentabilidad anual? Pues muy fácil: le está intentando engañar. Como mínimo es un charlatán ignorante que no es consciente de la imposibilidad de lo que promete. Como máximo, es un estafador profesional muy consciente de que vende humo y promete lo imposible.
Insisto en interiorizar muy bien estos números, y les recuerdo el primer post de esta serie donde indagué por primera vez en la rentabilidad que podemos esperar sacar a largo plazo, planteando la asimetría de pérdidas y ganancias, las rachas malas que siempre llegan, y la observación de lo que han sido capaces de generar los grandes genios de las finanzas. Espero que con este segundo artículo y estos números muy concretos, se entienda todavía mejor la enorme dificultad de ganar más de un 20% anual, y lo que ello implica.
Por si acaso, lo voy a decir aún más claro:
- Si eres capaz de ganar un 10% al año de forma sostenida a largo plazo, eres bueno.
- Si eres capaz de ganar un 15% anual, eres muy bueno.
- Si eres capaz de ganar un 20% anual, eres muy, pero que muy, muy bueno. Tan bueno que quizá seas un gurú tipo Warren Buffet ó George Soros.
- Si eres capaz de ganar un 30% al año, eres un puto crack, un genio mundial de las finanzas, que además está teniendo mucha buena suerte. Dios te ama.
- Si eres capaz de ganar un 40% anual durante más de dos décadas, eres un farsante y mentiroso.
Igual me equivoco y existe alguna excepción, o hay alguna manera de rodear esta realidad, pero hasta nueva orden, debemos plantarnos aquí y considerar que estamos ante una gran verdad, un dogma de fe de las finanzas. Soy consciente de la simplificación de todo esto, pero por ahí van los tiros, por eso juego un poco a ser provocador.
La única manera de hacerse rico a largo plazo invirtiendo (al menos lo suficiente para alcanzar la independencia financiera), es utilizar la magia de la Ley de Capitalización compuesta, que aparecea largo plazo. Si algún año tenemos suerte y damos un pelotazo, estupendo. Pero ese no debe ser el objetivo, y con estos números que hemos visto espero que todo el mundo tenga ya claro que la clave es la paciencia, la constancia, y tener un horizonte de largo plazo.
Nos queda un último detalle que mencionar: analizar el impacto de las pérdidas, para asentar muy bien la importancia de protegernos de las pérdidas como objetivo número uno (y nº 2...porque en realidad no hay otro objetivo: todo lo demás se deriva de esto).
El impacto de un mal año.
La Ley exponencial se basa en reinvertir cada año los beneficios obtenidos. Un 10% sobre 30.000€ nos hace ganar 3.000€. Pero después de 20 años de inversión, un 10% sobre un capital acumulado de 500.000€ supone 50.000€ de ganancia.
En el próximo artículo mostraré cómo podemos alcanzar la libertad e independencia financiera en un plazo razonable (20/30 años, según nuestro capital inicial y nuestra capacidad de ahorro mensual), que nos garantiza en cualquier caso que podamos tener una muy confortable jubilación. Nadie quiere ser como Warren Buffet, eso es pura ilusión, una "idea", un símbolo, que tanto nos gustan a los seres humanos; a los niños les gustan los cuentos, que transmiten ideas y mensajes generales, y a los adultos les gustan las cabezas de turco y los ídolos, que viene a ser algo muy parecido...
Pero lo que dice Buffet son grandes verdades que podemos aplicar a nuestra escala, y que son válidos en realidad para cualquier método de inversión. No hay excepción: todos los ganadores de largo plazo comparten un perfil ultra-defensivo, porque sólo teniendo un mimo muy especial para nuestro capital, siendo muy prudentes y conservadores, conseguiremos atravesar las violentas crisis que periódicamente sacuden los mercados. En caso contrario, alguna de estas tormentas nos hará naufragar, y el viaje habrá terminado para nosotros.
Veamos a continuación el impacto que tienen las pérdidas a largo plazo. Se trata de otra forma de ver el funcionamiento de la LCC: queremos ver qué consecuencias tiene un mal año, sobre nuestro capital final (tras 25 años).
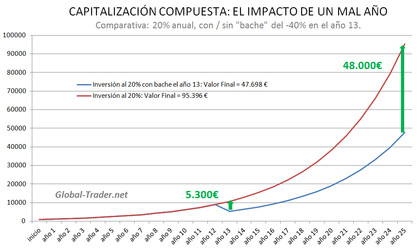
En el siguiente gráfico comparamos dos curvas: la primera es "sin accidente", y la segunda es "con accidente" en el año 13, donde perdemos un 40% del capital. En ambos casos vamos obteniendo un 20% medio anual (sobre un capital inicial de tan sólo 1.000€), salvo en la curva dos, donde el año 13 en vez de subir un 20%, caemos un 40%. Recuerden que el "drawdown" (Pérdida máxima ó peor racha posible) es aproximadamente del doble de la rentabilidad media anual que queramos obtener.
¿Qué ocurre? Pues que la pérdida del año 13 que es de 5.300€ aproximadamente, se transforma en unos 48.000€ que dejamos de teneral final de los 25 años. Lo que en un principio parecía una accidente grave, pero recuperable, al final resulta tener un impacto considerable. Ese es el impacto de una pérdida a largo plazo, y es la poderosa razón por la que nuestro foco de atención debe estar siempre en evitar las pérdidas (lo demás vendrá por añadidura si hacemos las cosas "normalmente" bien).
En el próximo artículo plantearé un plan de capitalización a largo plazo, utilizando todos los conceptos explicados hasta ahora, con números reales y factibles, y con varios escenarios en función de la rentabilidad esperada y de la capacidad de ahorro de cada cual. Es decir, plantearemos distintas vías para alcanzar la independencia financiera, con ó sin capital inicial, y para distintos niveles de ahorro.
Anexo.
Respuestas:
Adivinanza nenúfar:
al cabo de 31 días (al día siguiente duplica su tamaño).
a.
100€ al 10% anual durante 100 años = 100 * (1,10)^100 =1.378.061 €
b.
1000€ al 30% anual durante 50 años =497.929.223 €
c.
1€ al 2% anual durante 2014 años = 1 * (1,02)^2014 =209.288.771.386.200.000 €
Sí sí, has leído bien. Un euro invertido al 2% durante 2014 años, son más de 200.000 Billones (millones de millones).
¿Te has quedado corto ó te has pasado?
Normalmente el 90% de la gente se queda muy, pero que muy corto, porque más allá de 10 años perdemos toda la noción del tamaño. Simplemente se nos escapa de las manos.
"Si eres capaz de ganar un 40% anual durante más de dos décadas, eres un farsante y mentiroso. Igual me equivoco y existe alguna excepción"
No te equivocas, en absoluto. Y mira que hay fantasmas que fardan de estas rentabilidades...
Claro, siempre hay alguien que se sale del mapa. Lo difícil es encontrar alguien que se salga del mapa durante al menos 10 años seguidos...
Saludos!
De todas maneras cada individuo vive su realidad, yo utilizo por ahora en una cuenta un capital de 200 euros apalancao 300 veces, el Dax hace rangos de mas de mil puntos diarios,solo 10 puntos es un 33% de rentabilidad, para mi coger 10 puntos es un" juego de niños", el hacerlo acumulativamente es una cosa que voy a empezar hacer en cuanto me libere un poco de mis obligaciones, me probé un poco en la trading cup en la primera semana terminé superando un 50%Acumulativamente durante 5 dias hice lo que se hacer sin más,hay que tener en cuenta la condicion del individuo, yo opero sin dinero y el potencial que observo es de vertigo", tal vez sea un iluso,pero lo prefiero ser en este caso,porque no me limita y dependo exclusivamente de mi, no de datos macros o micros. Un Saludo
sin duda, si hay una forma de darle la vuelta a mi argumentación, ese es el intradia. Pero los peligros son muchos. Es algo reservado a una minoría dentro de la minoria. Las estadísticas son aplastantes. El 95% de los operadores intradia pierden tanto dinero que se retiran en menos de un año. Así que ya nos contarás cómo te va cuando empieces a reinvertir beneficios y asumir más riesgos... Suerte !
El riesgo es perder 200 euros, mis entradas son para perder unos escasos tic, puedo tener excepcionalmente hasta 4 fallos y en el quinto cogerlo y ganar dinero con solo un acierto, normalmente lo pillo a la primera en ocasiones a la segunda, entrando por entrar pero ejecutando con disciplina no me descapitalizo ni a tiros, a un a si, termino ganando, simplemente porque la disciplina se convierte en hábito, el hecho de acumular no veo mas riesgo sigue siendo el mismo.
En respuesta a Niko Garnier
Antiguo Usuario... ¿Se habrá hecho rico ya?
La pregunta es si "n" es el nº de años,meses o días y por qué.
n puede ser lo que tú quieras. Si tomas meses en vez de años, la rentabilidad será mensual.
De hecho en el próximo artículo de la serie plantearé escenarios con aportaciones (ahorro) y rentabilidades mensuales.
Saludos
Einstein decía que el cerebro humano no está preparado para entender el crecimiento exponencial, no le faltaba razón.
Tu artículo está muy bien pero olvidas una cosa muy importante, si además hacemos aportaciones mensuales o anuales regularmente, la gráfica se dispara aún más, y la independencia financiera está al alcance mucho antes. No solo está muy bien aprovecharse del interés compuesto poniendo una inversión inicial, sino ir aportando poco a poco a medida que podemos.
Es una pena que a la gente no le enseñen estas cosas en el colegio, seríamos una sociedad mucho más avanzada y todos trabajaríamos muchos menos años...
Nuestro cerebro no esta preparado para coger dinero de forma facil de los rios de dinero que son los mercados financieros.
No me olvido. Eso está previsto para el siguiente artículo ;)
Aquí quería centrarme sólo en la ley de capitalización compuesta. En el siguiente post haré proyecciones de largo plazo incluyendo aportaciones mensuales. Ahí es donde la cosa empieza a ponerse muy interesante, porque como bien dices, la independencia financiera está más al alcance de lo que parece.
Totalmente de acuerdo también con lo que dices sobre la enseñanza en el colegio. A nuestra escala hacemos aquí formación y cultura financiera. Es nuestro granito de arena...
Un saludo!
Vaya, el comentario anterior era en respuesta a Arek...
Pepe, estoy de acuerdo en derrumbar barreras y prejuicios tontos, pero de ahí a decir que esto es fácil...hay un gran trecho. No se le puede perder nunca el respeto al mercado... Jeje
Un abrazo!
Lo que quiero decir efectivamente para mi es facil, los dificiles somos nosotros, al fin y al cabo los precios se desplazan y giran no hacen otra cosa todos los dias a todas horas es siempre lo mismo, es entrar en los giros sin mas, y para eso hay que hacerlo facil.
Hola, lo podrías explicar más detalladamente. Tengo amigos que han leído mil libros y han hecho cursos de intradía y no son consistentes en sus ganancias ni independencia financiera ni nada, por supuesto. Y tú dices que es "fácil y que entras en los giros". Encima sin indicadores ni análisis técnico ni nada. Encantado de que lo expliques en detalle si no es molestia. Saludos.
No es molestia, el intradia cuesta hacerlo bien porque vamos contaminados con el largo plazo, no vale posicionarse y mantener una posicion perdedora, por eso hay que cogerlo desde muy abajo y el Stop tiene que estar al lado, nada de ponerlo lejano, y de esta manera se evitan las operaciones al azar. Yo fallo uno o dos o qizas tres y con una buena es suficiente para salir victorioso en un dia malo, no sois consistentes por que dais demasiada ventaja al mercado y os quedais en una situacion fragil con stop lejanos,el stop lejano esta bien para el medio plazo pero para el intradia no vale , hay que posicionar se cerca de los giros, empaparse en la cultura de los fallos bajistas o alcista, a las redistencias hay que estar ya posicionados con beneficios por si rompe y añadir mas contratosy para abajo lo mismo, cuando los indices son alcistas hay que tener cuidado con abrir cortos en roturas de soportes porque te pueden barrer, por eso ya hay que ir ganando a los soportes , ya estoy cansado jeje espero que te sirva de inspiracion
Muy importante son los maximos y minimos del dia anterior
en el tema de la cultura financiera en los colegios, realmente quien tiene cultura financiera?los cultos en esto con muchos estudios financieros que gestionan fondos cuando les va mal dicen que es cuyuntural, debe de ser una palabra magica al alcance de unos pocos, ja.ja
La cultura financiera es un concepto amplio. No se refiere únicamente a conocimientos económicos estadísticos o matemáticos. El conocimiento es vital y debe abarcar todas las ramas de la sabiduría humana. Se debe saber de sociología, psicología, geopolítica, macroeconomía y además mucho sentido común y suerte. Conforme mejor domines la situación podrás asumir riesgos mayores y aprovechar los grandes vaivenes y crisis cíclicas que se producen en la sociedad capitalista.
De todas formas, cada uno ha de conocerse lo mejor posible y actuar siguiendo su propio carácter. Aquí caben muchos caminos hacia una misma meta.
Un saludo.
Claro que la cultura financiera es un concepto amplio. Pero como la cultura en general, sólo una parte muy pequeña de ella sirve para ganar dinero de forma clara y decisiva. Lo cual no significa que el resto no sea importante e interesante.
Por otra parte, la cultura es también es un concepto amplio y ambiguo, muy ligado a la ideología, y ahí es donde el ser humano se pierde en mil batallas absurdas, porque la mayoría de la gente no es consciente de cómo influyen sus prejuicios en sus razonamientos. Es un tema complicado y delicado, lo que quería decir aquí es que no se soluciona el problema de la cultura general afirmando que 'hay que formarse y aprender'. No hay más que ver las reformas educativas desde hace 20 años...
Para bien y para mal, el saber no es algo objetivo, no hay un manual que estudiar y ya. Algunas personas estudian y aprenden bien, y otras muchas se extravían en el camino, aprenden conceptos equivocados y acaban peor que otros que en teoría tienen menos cultura.
Termino con una pregunta abierta: ¿qué relación hay entre cultura y sabiduría? ¿Se puede tener sabiduría sin tener cultura? ¿Se puede ser culto pero nada sabio? Yo pienso que sí. Es mejor ser sabio que culto. Algo de cultura hay que tener para ser sabio, pero me atrevería a decir que los que tienen mucha cultura no son precisamente los más sabios...
En fin.
Saludos!
Yo creo que un sabio es una persona muy inteligente con poca cultura y conocimientos, lo soluciona con sabiduria, otra muy culta y con muchos conocimientos, no necesita ser sabio e ingenioso, para que?, por eso antiguamente habia tantos sabios.
Bajo mi entender uno de los pecados de la actual situación comercial en la industria de la bolsa, vendedores de curso, libros, web es precisamente vender la idea de 1) trading e inversiones como profesión 2) como solución al paro ( ojo si al paro) 3) y el objetivo ansiado de libertad financiera ( poder dejar un trabajo que no gusta etc etc).
Particularmente pienso que es esa ansiedad a querer sacarse un sueldo de esto, o al querer ir demasiado rápido la que propina grandes ruinas bursátiles al pueblo.
Por poner un ejemplo aunque inviertas en derivados, o operaciones arriesgadas una gestión de riesgo consecuente no te permitirá excesivos riesgos y apancamientos, una cosa es tener suerte y doblar una posición en un activo o valor dentro de una gestión de cartera que puede ser un 3 o 5% de lo anual, y otra obtener un 40%, mi experiencia me dice de gente que ha obtenido estos márgenes de repente un año fracasan.
En esta carrera de libertad financiera solo hay dos caminos arriesgar bajo riesgo de que el mercado te deje fuera para siempre o un largo tiempo o ir poco a poco.
La ansiedad por un sueldo o exceso empeño en libertad financiera no es una buena sicología para el trading porque te crearía nervios y seguramente equivocaciones de querer operar para ganarle al mercado.
A mi solo se me ocurre una idea para poder conseguir un triunfo sin demasiado coste de riesgo, y aun asi hay un % de suerte, ya la comentare algún dia.
Son estrategias demasiado apalancadas sobre beneficios ya obtenidos para no tener riesgo de perdidas, y aun asi habría que tener mucha suerte, porque este tipo de operativas tendrías que acertar un movimiento amplio en muy poco espacio de tiempo, y casi mejor cercano al vencimiento.
Es algo parecido a decir si he sacado a una operación un 8% el 4 % lo arriesgo a un derivado casi imposible por lo sorpresivo, algo parecido al que haya acertado la bajada del crude con derivados, dependiendo de su apalancamiento puede haber tenido un beneficio tan brutal que le haría tener opción a la libertad financiera, pero además harian falta mas operaciones de este tipo, no muchas pero quizás acertar de 5 a 7 veces movimientos parecidos en activos.
Y luego esta el tema de la capitalización compuesta, pero claro a márgenes normales un 4 a 5% de medua contando con años de un 10 a 20 % y años de un 0 o perdidas uno terminaría libre financieramente pero ya siendo un viejo, el tema es conseguir esto joven, al menos con menos de 50 para disfrutar de la vida.
Saludos
Joder, Juan no nos quites la ilusión, mientras luchamos por conseguir nuestros sueños vivimos con ilusión, la vida es eso ilusión y si encima lo consigues pues de puta madre, jaja.
La sabiduría en un sentido amplio es un fin en sí misma. Sabiduría implica conocer de verdad que es lo que te importa. Dentro de ello estaría también el conocer el mundo financiero, ya que el manejo del mundo del dinero te puede dar mayor libertad a la hora de aprovechar lo valioso de la vida. Además como actividad hay que reconocer que es atrayente y un reto para la actividad intelectual.
En cuanto a la edad, es muy relativo, lo importante es ir viviendo, avanzando en la vida, creando tu familia y marcándote retos. No debes tener prisa por ganar dinero y vivir. Debes vivir mientras vas ganando dinero. Es más éste es una herramienta que te ayuda pero no es el fin. El fin es la propia vida. La edad además es algo subjetivo. Si no estás enfermo, no disfrutas menos con 45 que con 25 años, es más por experiencia te digo que sabes apreciar mucho mejor todos los matices cuando has madurado.
Y además la inversión es una actividad que no decrece con la edad sino que incluso conforme pasan los años y aprendes de las situaciones y los reveses sufridos te haces mejor.
En fin, un mundo apasionante, una rama más de la sabiduría humana, que tiene eso sí la particularidad de que puedes recibir recompensas considerables o castigos dolorosos. Pero eso mismo en la inversión, no importa solo el hecho monetario de ganar 50 o 100, sino la aventura y la esperanza del reto.
Un saludo.
Muy de acuerdo.
El camino hacia la independencia financiera no debe ser estresante. Sin presión. Hacer las cosas bien, y no olvidar que como dijo John Lennon, "la vida es eso que pasa mientras haces planes de futuro".
No es incompatible vivir tu vida y hacer las cosas bien, con cabeza, pensando en el futuro. Disfrutar del camino pero sabiendo a dónde vas y tratando de mantener el control, asumiendo con sabiduría que no lo podemos controlar todo y siempre hay una parte de nuestro destino que no depende de nosotros. Se trata de hacer al menos las cosas bien en la parte que depende de nosotros, y eso pasa por tener un buen conocimiento de partida...
Saludos
También es el marketing de toda esta industria generar ilusión, todo hay que decirlo, solo hay que ver muchos libros de bolsa y mercados y lo que venden, asi como ciertos profesionales, creo que en este sentido hay que ir paso paso sin crearse objetivos de % .
Esto es como una carrera de galgos la pellica son Bufett y compania, curiosamente siempre son los mismos, no aparecen nuevos genios de los mercados, llevan años contando como lo hacen, y generan ilusion, pero Buffet cuando se muera , quien es el siguiente Bufett? , ahora todos son muy buenos sobre todo la gente joven que solamente conocen un mercado alcista .
Mi ilusion es que con ciertos ingredientes que yo tengo pueda crear algo, el gazpacho se hace con ingredientes no con la apariencia, de todas maneras para conocer los mercados de alguna manera tienes que pasar por el aro"

