El pasado viernes, tras una jornada de debate sobre la obra de Mises «La acción
humana» (evento organizado por el Círculo Hazlitt en Málaga), alguien comentó que la bolsa es un juego de suma cero.
Personalmente no comparto esa opinión. El objetivo del
presente artículo consistirá en argumentar mi desacuerdo.
Antes de comenzar, expliquemos en qué
consiste un juego de suma cero:
Un juego de suma cero es un juego no
cooperativo donde la riqueza está dada. Tras jugarlo, las
ganancias que uno obtiene se
corresponderían con las pérdidas de otro. Un ejemplo de
juego de suma cero sería el póquer o juegos de mesa como el
ajedrez donde siempre habrá ganadores y perdedores.
¿Por qué la bolsa no es un juego de
suma cero?
El hecho de que se compare la bolsa con
los juegos de azar, quizás sea la razón principal por la que
es considerada un juego de suma cero. Parecería que para
lograr altas rentabilidades invirtiendo, otra persona debería sufrir
fuertes pérdidas. Resulta que esto no es así: la
compra/venta de acciones no se diferencia en nada a la compra/venta
de otro activo, como por ejemplo podría ser una vivienda, o a la
compra/venta de bienes y servicios.
Si comprar una barra de pan se
considera un juego win-win (el intercambio resulta beneficioso
para ambas partes), comprar o vender una acción no debería tener
una consideración distinta. No es más que otro intercambio
voluntario realizado en el mercado. También puede verse cómo la
cotización del conjunto de todas las acciones de una economía no
está limitada: el agregado de las mismas puede subir.
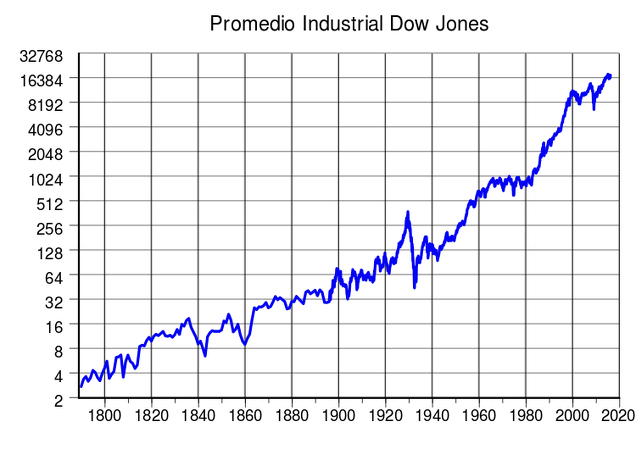
Gráfico histórico del PromedioIndustrial Dow Jones (1789-2016). Fuente: wikipedia.
Si una empresa atiende correctamente
las necesidades de sus clientes, la misma puede crecer. Por tanto
genera valor, o lo que es lo mismo, se crea riqueza.
Podemos ver como ejemplo la evolución que ha seguido el precio de
las acciones de Amazon:
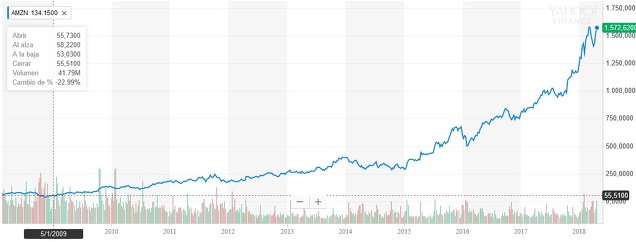
Fuente: Yahoo Finanzas.
En la bolsa la riqueza no está
dada: las empresas que cotizan en la misma podrán subir e
incluso bajar hasta desaparecer. Las empresas pueden crear riqueza.
Quien vende una acción no es automáticamente el perdedor de un
juego, como tampoco podemos ver al que la compra como el ganador. En
el momento de realizar la transacción ambas partes consideran
subjetivamente que salen ganando con la misma: quien vende valora
más el dinero que la acción, y quien compra valora más la acción
que el dinero entregado a cambio de la misma.
Un inversor que decida vender puede
hacerlo por múltiples razones:
- Porque ha encontrado otra
opción mejor.
- Porque en ese momento necesita
liquidez (lo que no quiere decir que no haya obtenido un
rendimiento positivo y haya logrado vender la acción más cara de
lo que la compró).
- Porque su horizonte temporal no
es el adecuado.
- O por ejemplo, porque según su
análisis considera que la acción ha alcanzado su máximo
potencial.
Por el contrario, quien compra una
acción opina que la misma dispone
aún de margen suficiente para
continuar creciendo. En definitiva, espero que haya quedado
medianamente claro por qué pienso que la bolsa no puede ser
considerada un juego de suma cero. Caso aparte sería el mercado
de derivados (opciones, futuros, etc.), del que efectivamente
podemos afirmar que se parece bastante al de las apuestas
deportivas. En un mercado de derivados existe una contraparte,
la cual 'apostará' por que va
a suceder lo contrario de la posición hayamos tomado
nosotros. Esto quiere decir que hay ganadores y perdedores:
unos se llevarán lo que otros han perdido. Sin embargo, no se
debería demonizar por ello a estos productos: los derivados ayudan a
reducir riesgos y a diversificar…
aunque ésta sería ya otra historia. Lo dejamos aquí.
Un saludo y hasta la próxima.
En teoría la bolsa sí es un juego de suma cero porque una empresa tiene un numero limitado de acciones y para que tu puedas comprar las que deseas necesitas una contraparte que te de las acciones que deseas de manera que si esto no ocuriera por falta de liquidez incurriría en un desplazamiento del precio en tu contra por tú interés comprador. Digamos que los cachos de tarta son constantes por lo que dependes de una contraparte que venda algo que ya hay. Pero en la práctica sabemos que no es de suma cero porque la empresa si genera beneficios esos beneficios se reparten entre todos los accionistas y se podría dar una situación donde todos ganen.
Por el contrario, hay productos como los pares de divisas donde tus ganancias dependen exclusivamente de quitarle las ganancias a otro, es más, se podría decir que es un juego de suma negativa pues las comisiones de los brókers quitan parte del pastel continuamente, como en una mesa de póker que tiene comisiones. Llega un momento que todo se lo queda la banca.
En respuesta a Mister killer
Gracias por comentar, Mister killer
La mayor o menor escasez de un producto no es lo que determina que un juego sea de suma cero o positiva. Como tampoco el hecho de que sea más o menos líquido. Si se fija, en todo intercambio existe una contraparte. Si Vd. desea vender naranjas, necesita de otra persona para que se las compre. Si no logra vender su mercancía, por muy buena que ésta sea, deberá proceder a bajar el precio.
Si Vd. puja por una acción y el precio comienza a subir, y pese a ello, sigue considerando que es interesante pagar lo que le piden, es porque Vd. piensa vale más de lo que pagó. Claro ejemplo de juego de suma posiva. Lo que determina que un juego sea de suma cero o no, es si lo que uno pierde coincide exactamente con lo que otro gana. Si la compra/venta de acciones es un juego de suma cero, entonces lo sería la compra/venta de cualquier mercancía.
Buen punto lo de la suma negativa: ciertamente si tenemos en cuenta la comisiones, los derivados podrían meterse en dicha categoría :)
Un saludo.
En respuesta a Mister killer
¿Suma cero?, o ¿carrera de relevos?.La empresa tiene beneficios y sube, vendes, ganas, alguien compra, y sigue dando beneficios y sigue subiendo, ¿cuando se pierde?.
En respuesta a Mario Gutiérrez Mata
Puedes hablarme de tú sin problema alguno jejeje, si tardo en responder es porque tengo la cabeza en muchas cosas.
Pues eso te iba a comentar en un juego de suma cero uno gana lo que pierde el otro. Si yo compro una barra, a cambio pierdo los centimos que me cueste y el panadero pierde la barra de pan. Si en algun caso especulara con la barra de pan y se la vendiera a un tercero yo sacaría un posible beneficio respecto al primer vendedor gracias a un ineficiencia que he descubierto, pero la suma seguiría siendo cero en el juego, hay dos partes que ganan y pierden.
En las empresas en teoría es igual, pero lo cierto es que a diferencia de derivados como los que he expuesto si la empresa gana anualmente unos beneficios que reparte esos beneficios hacen que la suma no sea cero, en cambio si el intercambio de acciones se hace en el corto plazo sí sería de suma cero pues no da lugar a que se reciban dichos beneficios.
En respuesta a Mister killer
¡Ah! Ok. Entonces es en este punto donde estamos en desacuerdo :)
Yo parto de la siguiente premisa:
Para que se produzca un intercambio, es condición necesaria que se valore más lo que se va a recibir que lo entregado.
Saludos.
El error puede venir de gente que usa la expresión “jugar en bolsa “ que viene de otros tiempos ya que ganar o perder era como una lotería.
Te la juegas. Si Compras un paquete de acciones, pueden subir, bajar, o ambas cosas. El paso del tiempo es crucial . Si compras una barra de pan, no. Lo compras, sabes lo que es, sobre todo si vas a la misma panadería porque te gusta su pan. Win-Win. Compras unas acciones. ¿Compra un trozo de empresa, a su precio Justo? Nunca se sabe. En Bolsa siempre se está intentando anticiparse al momento siguiente. Warren Buffet: “si el mercado fuera eficiente, yo estaría pidiendo caridad por la calle”. Mmmm, ¿no implica eso ganadores perdedores?
Siempre hay asimetría en la información. Lo dejo aquí.
En respuesta a Miguel Navascues
Muchísimas gracias por su comentario, Sr. Navascues.
Evidentemente, la incertidumbre al comprar una acción algo superior… Es un producto mucho más complejo.
Saludos

