Resumen
Los mercados de acciones, desde un punto de vista operacional, son muy eficientes. Superar el rendimiento que ofrece en su conjunto, a través de la identificación y explotación sistemática de oportunidades a lo largo del tiempo, es la (diminuta) excepción dentro de un ecosistema donde la norma pasa por la extraordinaria dificultad que entraña superar al mercado. Los análisis y la evidencia confirman este punto de eficiencia operacional. El debate surge cuando se trata de explicar cómo y por qué emerge esta eficiencia. Cómo y por qué se mueven las cotizaciones. El enfoque ortodoxo, claro dominante desde mediados del siglo XX, encuentra respuesta al “cómo” en el azar, y al “por qué” en la racionalidad. Pero este enfoque es incompleto, porque no es capaz de dar respuesta a muchas dinámicas que se observan en los mercados de acciones. Hay algo más que no llega a explicar el azar y la racionalidad.
A lo largo del documento repaso la historia de cómo el azar ha llegado a ser el pilar sobre el que se han construido las principales teorías de carteras y modelos de valoración de activos. Y propongo complementar el enfoque aleatorio con un nuevo modelo, donde los sistemas complejos dan respuesta al “cómo”, y la ecología, el conductismo o las narrativas económicas aportan información para encontrar la respuesta al “por qué”. Para finalizar, desarrollo una metodología, que integra el enfoque de sistemas complejos y narrativas, con aplicaciones prácticas para la gestión de carteras.
En el mercado hay azar. Pero también complejidad. Debemos aprovechar los avances de las últimas décadas en la comprensión de sistemas complejos para reducir el número de hipótesis que derivan en análisis rectilíneos.
Porque “caminando en línea recta no puede uno llegar muy lejos”.
Mercados de acciones: un juego de azar
En el Liber de Ludo Aleae (Libro de los juegos de azar) del año 1565 encontramos uno de los primeros modelos matemáticos de precios utilizado en los mercados financieros. Su autor fue el famoso matemático italiano Girolamo Cardano, que también era filósofo, ingeniero y astrólogo. Cardano destaca la igualdad de condiciones como el principio más importante en el juego. Como señala el autor “En la medida en que, al alejarnos de esa igualdad de condiciones, damos ventaja al contrincante, estaremos siendo tontos y, si la ventaja es para nosotros, injustos”.
Este concepto de juego justo, sin trato de favor para ninguno de los contrincantes, es lo que se denomina martingala, y se encuentra en la base de muchos otros conceptos de las matemáticas y la física. La característica más importante de este tipo de juego es sencilla y con unas consecuencias de amplio espectro: no se puede prever lo que vas a ganar o perder basándote en tus pérdidas o ganancias pasadas.
En el año 1900, el entonces doctorando Louis Bachelier defendía su tesis Théorie de la Spéculation ante el tribunal examinador de la Universidad de París, entre los que se encontraba uno de los matemáticos más célebres de todos los tiempos, Henri Poincaré. En la tesis, el joven Bachelier analizaba los precios de los derechos de suscripción. Estos son contratos que conceden al titular el derecho, pero no la obligación, de comprar un valor a un determinado precio antes de una fecha establecida ¿Cuánto vale esa garantía? Esta es la pregunta clave para el inversor, y la respuesta es sencilla: dependerá de la evolución del precio del activo hasta la fecha de vencimiento. Su cálculo, bastante más complejo.
Bachelier no era el primer investigador que trabajaba en la identificación de patrones con los que anticipar las variaciones en las cotizaciones de las acciones. Pero sí fue el primero en hacer el siguiente razonamiento. Cada vez que se cruza un precio, hay detrás un comprador y un vendedor que han acordado la operación. Y esta operación ha de ser justa, porque nadie quiere ser el tonto de la película. En consecuencia, Bachelier concluyó que los precios de las acciones necesariamente deben variar de un modo completamente aleatorio, argumentando que un inversor nunca podía beneficiarse de la información que obtuviera estudiando patrones del pasado. Habida cuenta de que los movimientos aleatorios pasados de las cotizaciones en un mercado eran martingalas, entonces “la esperanza matemática del especulador era cero”. Era matemáticamente imposible ganarle la partida al mercado.
A falta de información que pueda modificar el equilibrio de la oferta y la demanda ¿cuál es la mejor predicción de la cotización de mañana? El precio puede subir o bajar, con grandes o pequeñas variaciones. Pero, a falta de información decisiva que modifique las condiciones, el precio se mantendrá fluctuando en torno al punto de partida. Y la mejor predicción del precio de mañana será el precio de hoy. Es más, cada variación del precio no guarda relación con el anterior. Es lo que se denomina en estadística una serie de variables aleatorias independientes e idénticamente distribuidas. Como el juego de cara o cruz con una moneda equilibrada. Las cotizaciones pasean de forma aleatoria a lo largo del tiempo.
Las intuiciones económicas de Bachelier permanecieron muchos años en el olvido. Su tesis, Théorie de la Speculation, se publicó por fin en 1914 con una buena acogida en el ámbito académico francés, pero sin excesivo entusiasmo. En aquellos años las finanzas eran un inmundo negocio, no un tema de investigación académica. Una actitud que empezó a cambiar tras el crack de 1929 y la Gran Depresión, catástrofe que sirvió de estímulo para que muchos economistas empezaran a intentar comprender los mercados financieros.
En el año 1954 la tesis doctoral de Bachelier cayó en manos de Leonard Jimmie Savage, importante profesor de estadística de la Universidad de Chicago, y envió cartas a varios colegas alertándolos de este diamante escondido. Entre los destinatarios estaba Paul A. Samuelson, uno de los economistas más influyentes del siglo XX. Como apunta Andrew Lo “no es ninguna exageración decir que la carta de Savage cambió el curso de la historia de las finanzas”.
Samuelson comprendió inmediatamente la importancia del trabajo de Bachelier y centró su investigación en el ámbito financiero a principios de la década de 1960, haciendo referencia a Bachelier en cursos, seminarios y clases magistrales que impartía. Pero, si bien Bachelier explicaba el cómo del paseo aleatorio, Samuelson se propuso explicar por qué las cotizaciones se comportaban como si fueran aleatorias. Y dio con la respuesta en el mercado de futuros de Chicago.
Samuelson identificó una paradoja: si la meteorología influía en el precio del grano ¿Cómo era posible que ese precio siguiera un curso aleatorio? Los patrones meteorológicos son complejos, pero no aleatorios, y las estaciones no siguen unas a otras de manera aleatoria. Resolvió esta paradoja sirviéndose de la técnica matemática de la inducción, de una forma rápida y elegante. Fue capaz de demostrar que el precio actual de un activo contenía toda la información sobre las variaciones pasadas del precio de este. El precio ya incorpora toda la información disponible sobre activo hasta ese momento: cambios meteorológicos, coste de almacenamiento, etc. Ya está todo recogido en el precio actual. Por lo tanto, las variaciones pasadas de precios no aportan información alguna sobre el precio futuro de los activos.
El razonamiento de Samuelson fue el siguiente: si los inversores son capaces de incorporar a día de hoy todos los impactos potenciales de acontecimientos futuros en el precio actual de un activo, entonces los precios futuros no se pueden predecir con la información actual porque, de ser así, los inversores ya habrían utilizado toda esa información. Por lo tanto, los precios deben variar de forma imprevisible. Es un concepto sutil, claramente ligado a la martingala de Cardano y el paseo aleatorio de Bachelier.
La idea de Bachelier de un “juego imparcial” estaba prendiendo, y los economistas reconocieron el valor práctico de la descripción de los mercados mediante las leyes de azar y el paseo aleatorio. En los años 60 y 70, Eugene F. Fama se encargó de situar esta descripción en un marco teórico más amplio y desarrolló la “hipótesis de los mercados eficientes”. Piedra angular sobre la que se ha construido las herramientas de gestión de riesgos y teoría de carteras más dominantes del siglo XX y lo que llevamos de XXI.
En 1965, con la publicación de su tesis doctoral, Fama explicó su teoría de los paseos aleatorios introduciendo por primera vez el término mercado eficiente en el léxico financiero:
Un mercado “eficiente” se define como uno en el que las grandes cantidades de agentes racionales, que se proponen maximizar su beneficio, compiten activamente, todos intentando predecir el valor de mercado futuro de los títulos, y en el que la información actual importante está disponible prácticamente de forma gratuita para todos los participantes… En un mercado eficiente, de media, la competencia hará que el pleno efecto de la información nueva sobre los valores intrínsecos se refleje instantáneamente en los precios actuales.
Fama resumió su versión de la Hipótesis de los Mercados Eficientes en un epigrama que se hizo famoso: en un mercado eficiente, “los precios reflejan toda la información disponible”.
Alcanzado el grado de madurez en todo el cuerpo teórico, con respuestas al cómo y por qué se mueven las cotizaciones, no tardarían en llegar las aplicaciones prácticas. El primer gran paso lo dio Harry Markowitz cuando se planteó como traducir en ecuaciones los conceptos de riesgo y recompensa. Y fue de gran ayuda que las respuestas al cómo y por qué fueran en aquella época azar y racional. Porque si se cumple que las series son aleatorias independientes e idénticamente distribuidas, entonces podremos usar la distribución normal, o campana de Gauss, para su estudio y modelización. Este es un aspecto fundamental, porque las propiedades de este tipo de distribución facilitan mucho la modelización y los métodos de estimación por mínimos cuadrados.
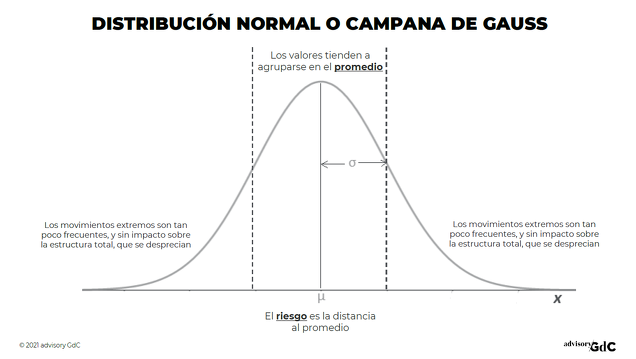
La recompensa, razonó Markowitz, depende del precio más probable de nuestra acción cuando llegue el momento de vender. Y “más probable” en la distribución normal significaría el promedio de todos los posibles precios antes de vender.
El riesgo es más difícil de definir. Markowitz pensó que una buena aproximación podría ser la amplitud de las oscilaciones del precio respecto al valor promedio. Las medidas más habituales de volatilidad en la campana de Gauss son la varianza y la desviación típica.
Ya tenemos un modelo media-varianza. Si añadimos varios títulos tendremos una cartera, y si tenemos en cuenta la correlación entre los títulos de la cartera, llegaremos a la Teoría de Carteras de Markowitz.
La relación lineal de Sharpe puede que sea la más usada en el ámbito de las finanzas. Partiendo de (i) la frontera de carteras eficientes de Markowitz, (ii) los supuestos, entre otros, de azar, racionalidad y (iii) relaciones causa-efecto determinadas por la linealidad, William Sharpe llegó a la respuesta para la pregunta ¿Cuál la rentabilidad esperada de la acción X?
Rentabilidad esperada = Rentabilidad sin riesgo + Beta x Prima Riesgo
Una solución simple y lineal, para una naturaleza que se supone simple y lineal. Donde los conceptos estadísticos van en aumento (varianza, covarianza, ahora la beta) gracias al sencillo campo de trabajo que permite la distribución normal.
El impacto del método de Sharpe (conocido por las siglas CAPM, Capital Asset Pricing Model) no fue evidente de entrada, ni para él. Hoy puede afirmarse que no hay escuela de negocios en el mundo donde no se enseñe este modelo, y no solo para valorar acciones. En la práctica, cada cálculo con el CAPM incorpora todo un ejército de asunciones añadidas, con lo que una respuesta pretendidamente objetiva puede volverse tan subjetiva como se quiera.
Con Markowitz y Sharpe primero, y otros muchos después, la inversión empezó a dejar de ser un juego de sugerencias y presentimientos para convertirse en una ingeniería de medias, varianzas, optimización e índices de aversión al riesgo. Las limitaciones computacionales de la época (década de los 50 y 60) era un inconveniente, pero el terreno ya estaba abonado. A medida que se avanzaba en la capacidad de cálculo, más respuestas se buscaban en estos modelos, sedientos de datos, matrices de varianzas-covarianzas, volatilidad, etc. Pero el problema surge cuando se olvidan las raíces y naturaleza de lo que se está estudiando: si el sistema o mercado rechaza las hipótesis de azar y racionalidad, el modelo puede tener dificultades.
Las principales teorías financieras y soluciones prácticas de los últimos ochenta años comparten ADN: azar y racionalidad. Pero está incompleto. Así lo confirma propia evolución del mercado, cuyo comportamiento en muchas ocasiones es imposible de explicar si solo tenemos en cuenta esa secuencia de ADN. La naturaleza del mercado no se puede resumir solo en una campana de Gauss. Hay más respuestas al cómo y por qué se mueven las cotizaciones, y las encontramos en los sistemas complejos.
Mercados de acciones: un sistema complejo
En los últimos años se está produciendo un replanteamiento de la supuesta aleatoriedad de ciertas series temporales, entre las que se encuentran las cotizaciones bursátiles. Dado que los sistemas complejos son capaces de generar dinámicas altamente irregulares, casi indistinguibles en muchos casos de procesos puramente aleatorios, cabe preguntarse si la “aparente aleatoriedad” procede de un sistemacomplejo. En caso afirmativo, aunque la predicción a largo medio y plazo está condenada al fracaso, será posible extraer información útil del sistema; al fin y al cabo, el sistema es determinista, por lo que existe algún tipo de regularidad que podremos incluir en nuestro proceso de toma de decisiones.
Los sistemas complejos pueden describirse a partir de un gran número de constituyentes básicos que interaccionan entre sí mediante reglas sencillas. A su vez, esas interacciones dan lugar a fenómenos nuevos, o “emergentes”, cuyas propiedades no pueden explicarse a partir del estudio de sus elementos constituyentes. Así, el comportamiento social de un hormiguero “emerge” de las interacciones entre las hormigas; lo mismo ocurre con el cerebro y las neuronas que lo forman, o con un ecosistema y las especies que lo integran. También con los mercados de acciones y los inversores que interactúan en la formación de precios.
El estudio de la complejidad es una teoría holística: es imposible comprender las características globales del sistema (mercado de acciones en nuestro caso) analizando por separado las partes que los componen. Esta naturaleza exige abandonar nuestra intuición lineal de los fenómenos y sustituirla por una visión del mundo basada en la no linealidad.
Los sistemas complejos aparecen a medio camino entre el orden y el desorden. Por una parte, el orden es necesario para almacenar información y mantener la estabilidad de las estructuras. Pero también se precisa flexibilidad para transmitir la información. La hipótesis de la frontera del caos, como se denomina, establece que la complejidad aparece en unas condiciones muy especiales: los puntos críticos en los que tiene lugar las transiciones de fase.
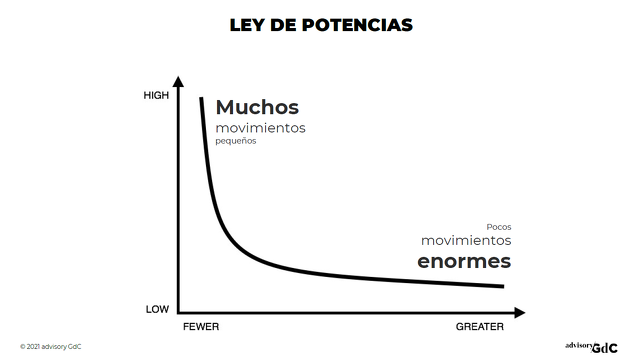
Numerosos fenómenos complejos, como los movimientos sísmicos, la macroevolución o los mercados de acciones, tienden de forma espontánea hacia el punto crítico. Del amplio abanico de funciones, solo hay unas pocas que se corresponden con el comportamiento de un sistema en el punto crítico: leyes de potencias y propiedades fractales. Dos características que se observan en las series de las cotizaciones bursátiles, destacando en este campo los trabajos de Benoît Mandelbrot y Xavier Gabaix.
En necesario, por tanto, completar el enfoque lineal y la distribución normal de los modelos de equilibrio, con el planteamiento no lineal y las leyes de potencias que nos llevan a los puntos críticos. Esta visión complementaria permite explicar muchos fenómenos de los mercados de acciones no encajan en la campana de Gauss. Un ejemplo son los movimientos extremos de las cotizaciones, clasificados como residuales y ruido blanco en la distribución normal, pero que la ley de potencias no desprecia al ser parte fundamental de su naturaleza.
El entorno: narrativas de inversión
El análisis de la complejidad es proclive a ser abordado desde una perspectiva de convergencia de ideas, conceptos y métodos que pueden considerarse comunes a varias disciplinas. También desde una proyección de confluencia de visiones en torno a dichas realidades desde diversos campos del conocimiento. El estudio de la complejidad favorece, por tanto, al enfoque interdisciplinar y multidisciplinar.
En el modelo que planteo, además de buscar apoyo en la teoría económica y financiera, toma apuntes de la psicología, el humanismo, la ecología, la física o la geometría.
Los componentes del modelo son: SEGUIR LEYENDO

