Un sábado más y la serie NUMB3RS me inspira a escribir métodos cuantitativos de finanzas en mi blog. Quien lo diría, con lo malo que era en matemáticas y lo poco que me gustaban cuando era pequeño. En este artículo vamos a hablar de algunos conceptos matemáticos que un lector mio (gracias Álvaro Romeo, te invito de nuevo a que me corrijas si hay errores para que todos podamos disfrutar de las matemáticas y el razonamiento logico/cuantitativo :P).

El coeficiente de correlación de Pearson nos permite determinar la relación lineal entre dos series de datos. El valor de dicho coeficiente varía entre -1 y 1. -1 si la correlación es inversa (cuando uno sube el otro baja), 1 si es directa y perfecta. Para más información tenéis la Wikipedia http://es.wikipedia.org/wiki/Coeficiente_de_correlaci%C3%B3n_de_Pearson en el apartado interpretación. Hay una formula de Excel que nos lo calcula.
Después tenemos el test de Student para determinar que nuestra hipotesis nula es cierta. En nuestro caso utilizariamos la formula de la wikipedia referente a diferentes tamaños muestrales, diferentes varianzas (http://es.wikipedia.org/wiki/Prueba_t_de_Student). Cuando habla del estimador sin sesgo de la varianza de las dos muestras, imagino que como nuestra muestra no es completa únicamente podemos tomar la varianza de la serie de datos que tenemos. Se realizaría con la función de varianza de Excel y se calcularía todo lo demás.
Para que os hagáis a la idea, la prueba de T-Student se utilizaría, por ejemplo, en el caso de que tengamos dos tratamientos, uno es una pastilla placebo y el otro es una pastilla con medicamentos buenos, entonces utilizamos un conjunto de pacientes y a uno de ellos le subministramos el placebo y a otros cuantos el medicamento bueno. Acto seguido miramos como mejoran (tomandoles la temperatura por ejemplo) para verificar si realmente hay diferencia entre los dos tratamientos. El problema es que no es necesario que el tamaño de los dos grupos sean iguales, ni que su varianza sea la misma.
Mi plan inicial era, en primer lugar, determinar la relación que hay en todas las combinaciones de todos los instrumentos financieros con un programa de ordenador y posteriormente verificar mediante el test de Student la significación estadística de dichas correlaciones detectadas anteriormente, para finalmente especular con ello.
Acto seguido me di cuenta de que, aunque hubiera una relación y fuera cuantificable y comprobable, solo podríamos utilizarla en el momento actual/presente, realmente lo que necesitamos es ver si la serie de datos va adelantada una respecto de la otra. El problema es que estas formulas no nos sirve (o eso creo, corregidme si no es cierto), porque no tratan los precios de cierre que les pasemos como si fueran una serie temporal, sino como si fueran una muestra de datos. Es como cuando estáis en una fábrica, haciendo tornillos y queréis calcular cual es su resistencia, es independiente del tiempo las muestras que tomáis, cosa que en nuestro caso no es así. Necesitamos que la formula tome el factor tiempo, como algo a tener en cuenta en la ecuación, debido a que nosotros si que nos importa que precio va primero y que precio después.
Entonces, pensando, me di cuenta que podríamos verificar las series de datos verificando la correlación estadística y mirar si una serie está adelantada o retrasada respecto a la anterior. Basicamente cogemos un gráfico y lo ponemos debajo otro con el que queramos compararlo (no se si lo visualazáis) y cogemos el gráfico de abajo y lo movemos a la izquierda o a la derecha para verificar si va adelantado o retrasado. Luego, utilizamos un ordenador y realizamos todas las posibles combinaciones entre todos los valores de las bolsas del mundo para verificar por ejemplo, si el Euro Dollar, está adelantado respecto a los indices, 1 sesión por ejemplo. Si es así, miramos que hoy baje el Euro Dollar y nos ponemos a corto a final de la sesión sabiendo que muy probablemente (con un cierto porcentaje de acierto) bajará.
Bueno, pues dándole vueltas a estas ideas, necesitaba una fórmula para detectar si una serie de datos iba adelantada o retrasada respecto a la siguiente y buscando en Google llegué al siguiente artículo donde aparece una fórmula utilizada en series temporales:
http://www.seh-lelha.org/tseries.htm
Esta aventura en búsqueda de teoremas matemáticos y conocimiento me ha llevado a encontrar cosas tan útiles como el filtro de Hodrick-Prescott utilizado para determinar la tendencia de series temporales y muy ámpliamente utilizado por actuarios para predecir el PIB:
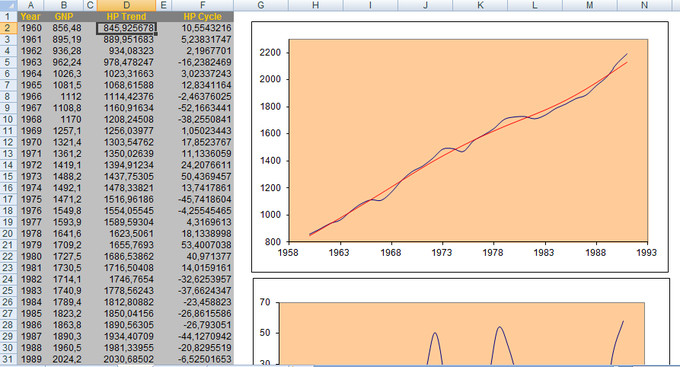
Como véis en la imagen es una media móvil pero muy fina y precisa (linea roja), tal vez pueda serles útil a los analistas técnicos si quieren investigar con ella, me parece fascinante.
Además leyendo la página www.seh-lelha.org me introdujo la función de autocorrelación, utilizada en series temporales para verificar la correlación entre dos series temporales distanciados un lapso de tiempo k. Eso era precisamente lo que buscaba, pero leyendo más abajo la propia página me introdujo en los métodos ARIMA para el análisis de series temporales. Las funciones ARIMA se pueden utilizar para predecir cual será el próximo valor de la serie de temporal. Os dejo un gráfico:
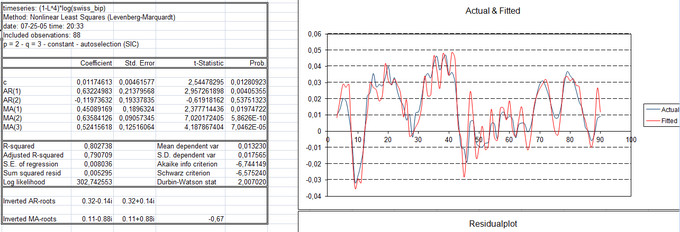
y una anotación para que se os haga la boca agua:
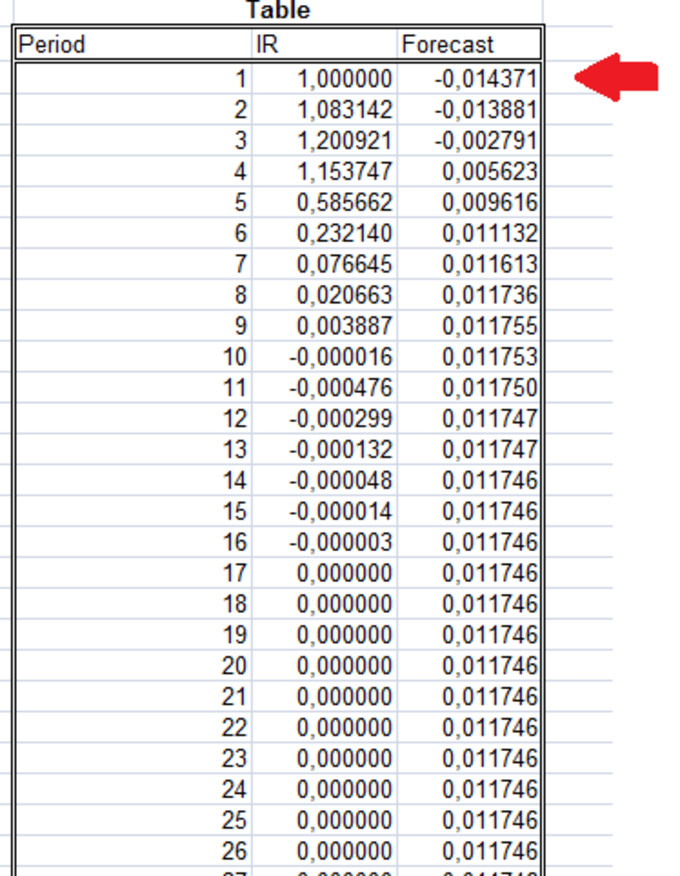
En ese caso, el valor que ha predecido es de la serie de pruebas, solo es necesario modificar la hoja de Excel y meterle los precios de la cotización de nuestros valores/indices favoritos, y verificar la precisión de esta herramienta. Si queréis, podéis hacerlo por mi y ya me contáis los resultados, mi tiempo es tan escaso útlimamente, podéis descargaros dichas hojas de calculo en la página www.web-reg.de. La idea es hacerlo 100 veces, con los 100 últimos precios, por ejemplo con una serie de datos semanal para verificar si acierta un porcentaje considerable de veces, si no en el puntuaje exacto, en la tendencia por lo menos para poder abrir largos/cortos según nos convenga.
Saludos y espero que paséis un buen fin de semana, yo voy a comerme mi pizza, que está a punto de salir del horno ¿os he dicho que es mi plato favorito?. ;)

