Sander Gerber, Harry M. Markowitz y Punit Pujara han escrito un nuevo paper llamado “Enhancing multi-asset portfolio construction under Modern Portfolio Theory with a robust co-movement measure” y se puede descargar aquí
Paralelamente, Corey Hoffstein comenta en su blog el nuevo paper de Harry M. Markowitz. A Corey le resulta interesante porque este paper nos recuerda que la asignación de activos es un problema no resuelto ya que incluso el padre de la teoría eficiente continúa explorando nuevas maneras de mejorar nuestros métodos.
En el paper se encargan de modificar la parte que se encarga de calcular la correlación entre los activos de la cartera. Ahora en vez de calcular la correlación de cada activo con respecto a otro, usa una matriz llamada Gerber Statistic y hace la siguiente función:
– La matriz va cogiendo pares de activos y va calculando el valor “M” que puede ser 1 o -1
– Si los dos rendimientos de cada activo son superiores a 0.5*su volatilidad o si los dos rendimientos de cada activo son inferiores a -0.5*su volatilidad, le asignamos a M el valor de 1
– Si los dos activos cumple solo uno de ellos la condición anterior, le asignamos a M el valor de -1
– El resultado final sera la división entre la suma de los valores de M de todos los activos, dividida entre el valor absoluto de M.
La formula extraída del paper es la siguiente:

Donde
-Ai es el rendimiento del activo A para el tiempo seleccionado i
-Bi es el rendimiento del activo B para el tiempo seleccionado i
– Ta es la volatilidad del activo A * su umbral escogido (0.5)
– Tb es la volatilidad del activo B * su umbral escogido (0.5)
– GS es el resultado de la formula.
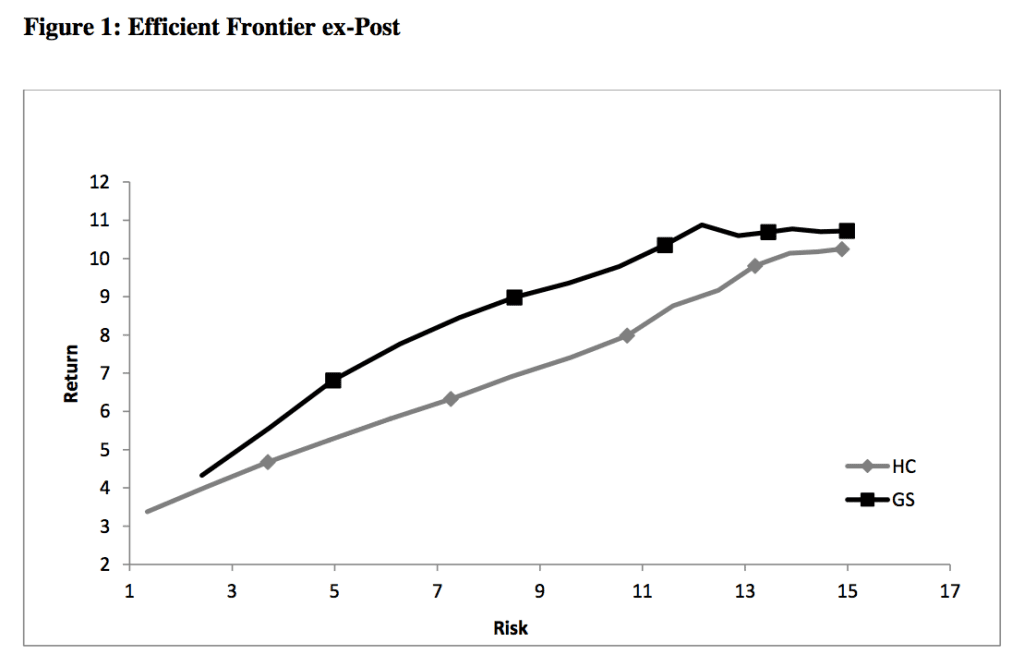
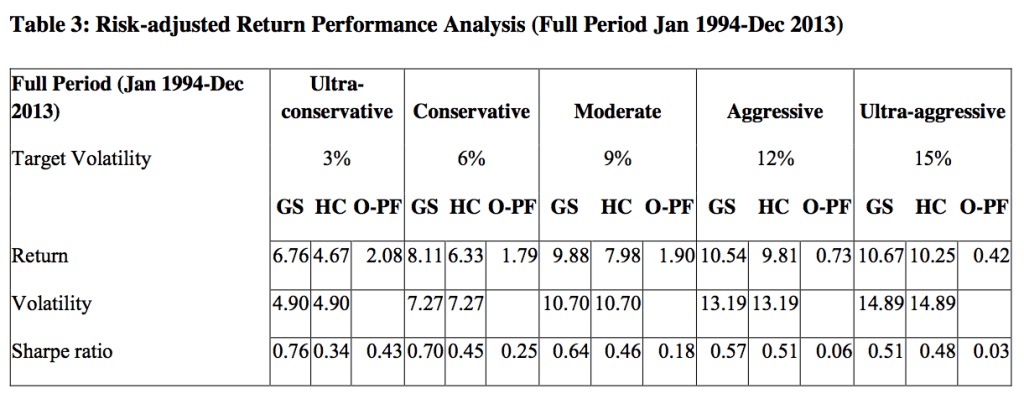
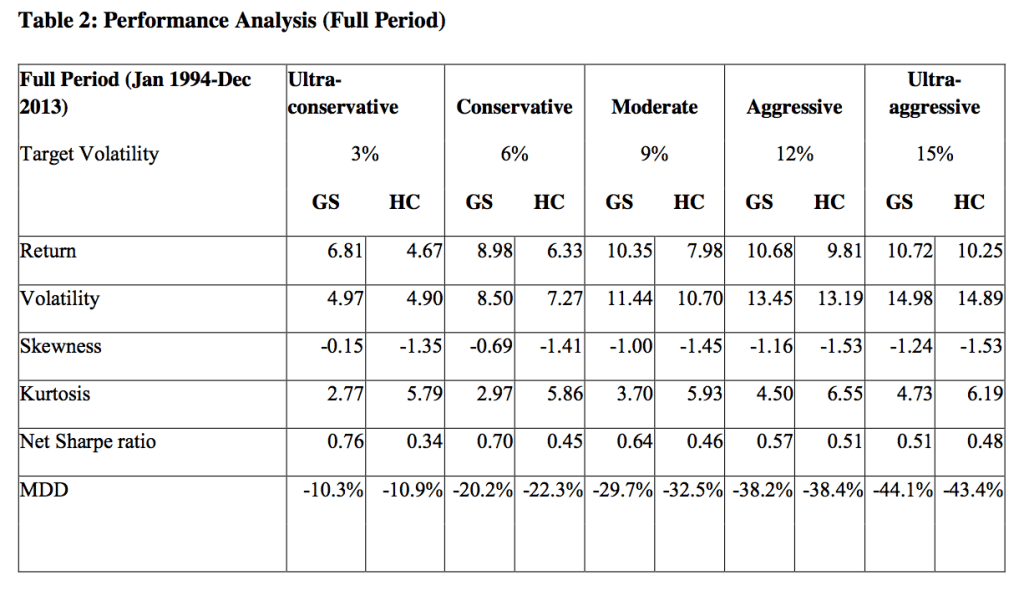
El autor simula desde el año 1994-2013 con multiples activos diversificados una cartera y compara los dos modelos, el original de la cartera eficiente y el nuevo sustituyendo el parametro de la correlación por la matriz de Gerber.
Según el grado de riesgo asumido se calculan todas las métricas y se puede observar que tanto el rendimiento, volatilidades, drawdown y ratio de Sharpe mejoran en todos los modelos.
A partir de esta nueva teoría se me ha ocurrido crear un código para calcular la matriz de Gerber para todos los activos que compongan el sistema. Para ello me he inspirado en la rutina que creó Sanz Prophet para calcular la matriz de correlación y que se usa en el sistema Flexible Asset Allocation:
function CalcPfC( symbol, tickerlist, length )
{
// This function takes a symbol and a list of symbols
// and calculates the average correlation of the
// symbols TS to the other symbols TS's (TS:TimeSeries)
CorSum = 0;
if ( tickerlist != “” )
{
for ( j = 0; ( ticker = StrExtract( tickerlist, j ) ) != “”; j++ )
{
data1 = Foreign( ticker, “C” );
data2 = Foreign( symbol, “C” );
CorSum = CorSum + Correlation( data1, data2, Length );
}
}
// take out the diagonal of the correlation matrix and average
PfC = ( CorSum – 1 ) / ( j – 1 );
return ( PfC );
}
Con el anterior código podremos calcular la correlación media de cada activo con el resto de ellos.
En el siguiente código que he creado calculara el valor GS que tendrá cada valor respecto a todos los demás:
//function GerberStat designed by Sergio Molina www.carterasdebolsa.com
function GerberStat (symbol,tickerlist,Length)
{
M = 0;
if ( tickerlist != “” )
{
for ( N = 0; ( ticker = StrExtract( tickerlist, N ) ) != “”; N++ )
{
data1 = Foreign( ticker, “C” );
ret1=ROC(data1,Length);
Vol1 = StDev( ROC( data1, 1 ), Length ) * sqrt( 252 );
data2 = Foreign( symbol, “C” );
ret2=ROC(data2,Length);
Vol2 = StDev( ROC( data2, 1 ), Length ) * sqrt( 252 );
M = M + IIf(((ret1>=0.5*Vol1) AND (ret2>=0.5*Vol2))OR((ret1<=-0.5*Vol1) AND (ret2<=-0.5*Vol2)),1,-1);
}
}
GS = ( M – 1 ) / ( N – 1 );
return ( GS );
}
Ahora solo me queda modificar el código FAA y modificar la parte de la correlación por la matriz de GerberStatistic y comparar los resultados, pero eso lo veremos en el siguiente post.
Saludos y perdón por el post tan teórico.
@Carterasdebolsa

