La
paradoja de corredor
El
filósofo griego Zenón de Elea, precipitó una crisis en la
Matemática antigua, estableciendo algunas paradojas ingeniosas, una
de ellas es la
llamada frecuentemente la paradoja
del corrredor, y que la
podemos resumir
de la manera siguiente:
Un
corredor no puede alcanzar nunca la meta porque siempre ha de
recorrer la mitad de una distancia, antes de recorrer la distancia
total. Es decir cuando haya recorrido la primera mitad, tendrá que
recorrer la segunda mitad. Cuando haya recorrido la mitad de ésta,
tendrá que recorrer la otra mitad. Cuando haya recorrido la mitad de
ésta, le quedará todavía la cuarta parte, cuando haya recorrido la
mitad de esta cuarta parte, le quedará la octava parte y así
sucesiva e indefinidamente.
Sin
embargo la experiencia física nos dice que el corredor que corre a
velocidad constante, alcanzará su meta en un tiempo doble del que
necesitaba para alcanzar su punto medio. Puesto que necesita T
minutos para la mitad del recorrido, habría de emplear 2T minutos
para el recorrido completo.
La
paradoja de Zenón, se podría explicar matemáticamente por la
teoría de series. Ésta distingue entre series cuyas sumas
parciales tienden a un límite finito (este sería el caso de la de
Zenón) y series cuyas sumas parciales no tienen límite finito
(este sería el caso en que la velocidad del corredor no permaneciese
constante, sino que decreciese gradualmente), es decir y según como
sea el límite, finito o infinito, hablaríamos de series
convergentes y divergentes.
Las
ondas de Elliott
Hoy
acercamos la teoría de Elliott a las matemáticas, y como siempre mi
amigo y vecino del 5º se preguntará, dónde encontramos la
conexión entre ambas. Seguidamente lo explicaré, a la vez que
aprovecharemos para dar la primera clase de la onda de Elliott.
La
teoría divide a las ondas en impulsivas y correctivas (hoy no toca
ver la terminales que, por otra parte, están comprendidas dentro de
las impulsivas).
Para
los que no están muy puestos en la teoría, diremos que una pauta
impulsiva es aquella que constan de 5 ondas (esto es de primero de
Elliott), de las cuales las ondas impares 1, 3 y 5 son impulsivas, y
las pares 2 y 4 correctivas.
Dicho
lo anterior, conviene recordar que, una pauta impulsiva consta de
tres ondas impulsivas de menor orden, así como a su vez éstas
contendrán otras tantas impulsivas de inferior orden. Enrique Santos
en su monografía sobre pautas impulsivas, equipara a éstas con las
matrioskas rusas (las típicas muñecas rusas que en su interior
contienen otras muñecas de menor tamaño). Y la pregunta que que se
nos viene a la cabeza al igual que en la paradoja de Zenón, es que
si se cumpliese esa serie ordenada de ondas, nunca llegaríamos a
ver el final de la pauta, y sin embargo (¡ a Dios gracias !) sí
tenemos el final de las pautas, o lo que es mejor todavía sus
correspondientes figuras de agotamiento (en próximos capítulos
intentaremos explicaros las figuras de agotamiento, tan importantes
por su valor operativo).
Ahora
es cuando al igual que en la paradoja de Zenón, las matemáticas
entran en juego para aclararnos que, las sumas parciales de estas
ondas impulsivas sí tienen un límite finito, y por tanto si se
completará ( yo añadiría, si el mercado lo tiene a bien) la pauta
desplegada y nos será posible buscar su agotamiento (siendo ésta
siempre la meta que buscamos, porque ese momento es lo mejor que nos
ofrece Elliott, operar en los agotamientos de las pautas).
Desde
que se inicia una onda 1ª (igual da que sea alcista que bajista) y
hasta la finalización de su onda 5ª y su posterior agotamiento,
nos valemos de otra serie, concretamente la de Fibonacci, serie que
debemos a otro de los grandes de la antigua matemática, como es
Leonardo de Pisa, cuya representación matemática es:
an
=an-1
+ an-2
Proyecciones
de las ondas impulsivas
Pero
cual sea su representación matemática, no es lo que más nos
interese para lo que nos ocupa, la importancia de este serie
matemática es que nos pone en bandeja las relaciones entre las
proyecciones de las diferentes ondas que componen las pautas
impulsivas y que podemos resumir en las siguientes:
A
) Del recorrido de la 1ª onda, podremos estimar por proyección, los
valores de la onda 3ª, siendo ésta en el modelo que mas nos gusta
encontrar (es decir de 3ª onda extendida que representamos como
X3), el 161,8% de la 1ª.
B
) De los recorridos de la ondas 1ª y 3ª, podremos estimar el
valor de la onda 5ª, siendo la zona en la que puede puede
encontrarse la 5ª, el intervalo comprendido entre el 100% de la 1ª
y el 61,8% de la onda 3ª.
Estas
serían las relaciones más frecuentes que se dan entre las ondas
impulsivas de una pauta de impulso.
Hemos
hablado de una forma muy ligera de lo que debemos entender por
“estimar”, ya que si bien en estadística se emplea este
término bajo unos parámetros científico matemáticos, no debemos
olvidar que, la teoría de Elliott no es ciencia (si bien siempre
repetimos que, a veces sí lo pareciera, por la exactitud de las
estimaciones), por lo que estas proyecciones no son el resultado de
ninguna ecuación matemática, debiendo dejar un margen de
fluctuación a juicio del analista.
Ya
hemos dicho, y en sucesivos artículos no nos cansaremos de repetirlo
que, de los modelos de pautas impulsivas, el que más nos gusta es
el de 3ª onda extendida (cierto es que si la extendida lo fuera la
1ª, nos hallaríamos ante una pauta terminal, y éstas si que son
nuestras preferidas, no en vano éstas dan el nombre a nuestro blog).
En cuanto al modelo de 5ª extendida no nos seduce porque, ni es
frecuente (la verdad es que es un modelo que se presenta contadas
veces), ni le damos mucha validez, ya que en ocasiones bajo este
modelo se pueden esconder recuentos erróneos (de todas formas
igualmente las relaciones de fibonacci entre sus ondas son muy
sencillas y ya haremos mención a éstas en el futuro).
Nos
hemos saltado las famosas siete reglas que Elliott establece para que
una onda pueda considerarse impulsiva, ya habrá tiempo más adelante
para enumerarlas y exponerlas, pues no queremos hacer más extensa
esta primera aproximación a las pautas de de Elliott, pero
prometemos que poco a poco iremos desmenuzando los conceptos que
consideramos más importante para poder especular con esta teoría.
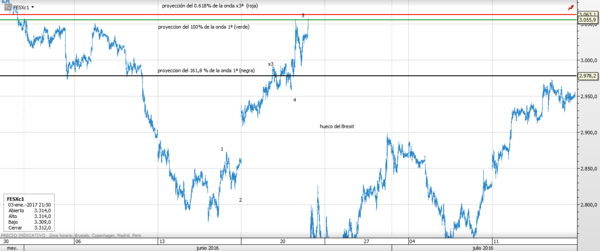
A
modo de ejemplo os adjuntamos la gráfica del futuro continuo del
eurostoxx en 5 minutos, en la que se puede apreciar perfectamente
como se han cumplido “milimétricamente” las relaciones de
Fibonacci que Elliott establece para las proyecciones de las ondas
3ª y 5ª.