En primer lugar
me gustaría presentarme. Soy Licenciado en Matemáticas y estoy iniciando mis
conocimientos en los Mercados Financieros. Desde hace varios años llevo interesándome por este
“caótico” mundo. Como humilde aprendiz que soy, mi objetivo no es otro que el
de seguir formándome y adaptándome a este entorno, a priori tan
diferente (o no) del que siempre me ha inspirado, las matemáticas.
En algunas ocasiones espero poder aportar la semilla a
nuevas formas de aproximarnos a la investigación de los mercados. En otras simplemente contaré curiosidades,
vivencias y recomendaciones personales, desde mi humilde posición.
Este mi primer
artículo, irá referido a la Ley de Benford (postulada en 1938 y demostrada en 1996), de la que tuve conocimiento al leer el libro "Un Matemático Invierte en Bolsa" de John Allen Paulos.
A grandes rasgos, la hipótesis consistía en que en una lista
aleatoria de datos lo suficientemente extensa, los números que comenzaban por un
“1” eran más frecuentes que los demás.
De modo más técnico y general, la probabilidad de que aparezca
la cifra “n” en el primer dígito de la lista es igual a
log10(n
+ 1) − log10(n) .
Mediante una hoja de Excel he calculado y representado estas
frecuencias :
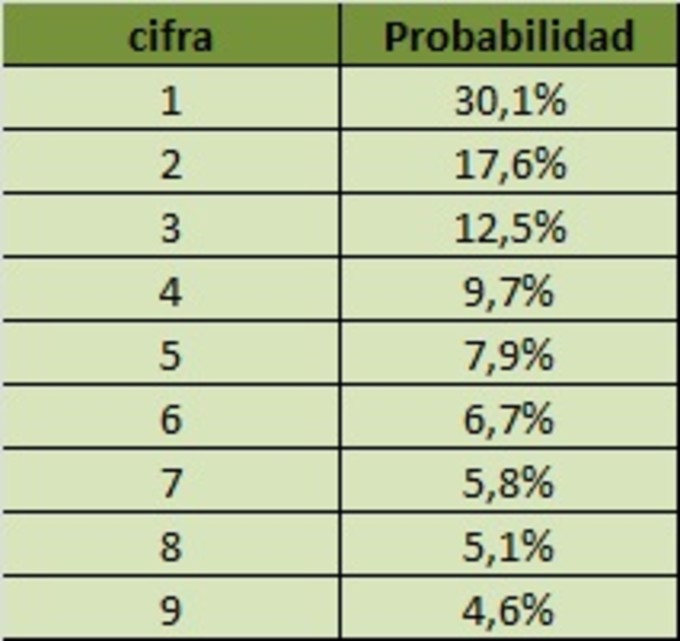
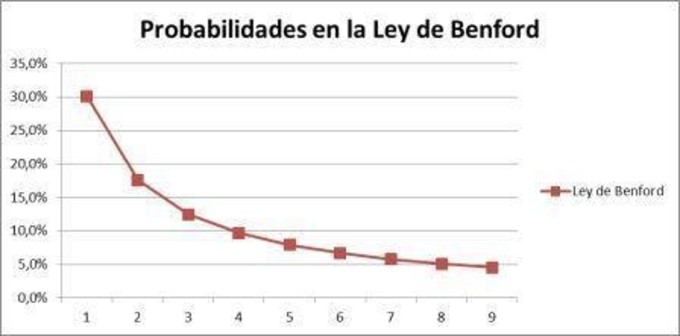
Resulta
prácticamente evidente decir, que esta propiedad no se verifica para cualquier
tipo de lista de datos numérica (por ejemplo si los datos siguen una
distribución uniforme). Además, dado que la Ley de Benford se cumple para listas
infinitas y que nosotros solemos trabajar con una cantidad finita de datos, la
tabla de frecuencias nunca será idéntica a la expuesta arriba sino que habrá un
margen de error, el cual tenderá a cero conforme nos aproximemos a un número
infinito de datos.
Estamos de enhorabuena, pues
resulta que estas probabilidades se cumplen en muy diferentes entornos
como son la naturaleza y la economía. Aquí he encontrado un ejemplo del cumplimiento de la Ley de Benford con datos demográficos : http://www.estadisticaparatodos.es/taller/benford/ejemplos_excel/poblacion_navarra.xls
Lo bueno de esto es que no es sólo una propiedad numérica, sino que tiene su aplicación práctica, véase para:
- Detectar el
fraude fiscal
- Probar el
“pucherazo” de las elecciones de Irán del 2009
- Descubrir (un poco tarde) la falsedad de los datos macroeconómicos aportados por Grecia a la Unión Europea para
entrar en la Euro Zona.
- Testear
observaciones del genoma humano
- Detectar el
fraude científico
- Etc.
Pues bien, mi idea es que podríamos hallar una aplicación práctica (o varias) al Mercado de Valores. Animo a la imaginación
del lector para proponer otro tipo de “experimentos”. Aquí va el mío.
Mi intención sería construir una base de datos en la
que incorporaría valores de diferentes Índices Bursátiles, así como sus precios
de cierre, en diferentes puntos extremos del índice. Posteriomente,
haría una comparación entre las frecuencias de aparición de cada cifra y las probabilidades de la Ley de Benford, en función del ciclo de mercado en el que
nos situemos.
Dada
la laboriosa tarea de recopilar todos los datos para este estudio, me voy a
limitar a mostraros mi idea con una lista muy reducida. Servirá esto para que
lo entiendan. El que lo desee y tenga tiempo podrá profundizar y añadir más
datos.
- Identificamos en el gráfico del
CAC-40 dos extremos de la gráfica
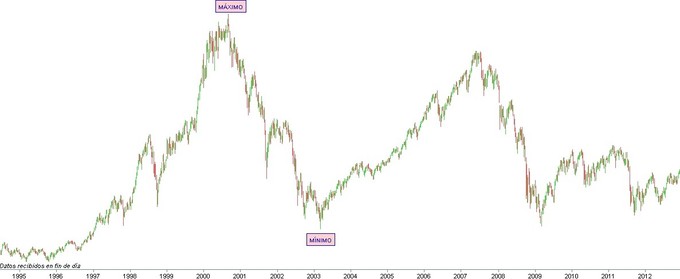
Las
fechas de cotización escogidas son el máximo histórico del 4 de Septiembre de 2000 y el mínimo del 10 de Septiembre de 2003.- Completamos nuestra tabla de datos
(muestro sólo algunas líneas por razones de espacio)
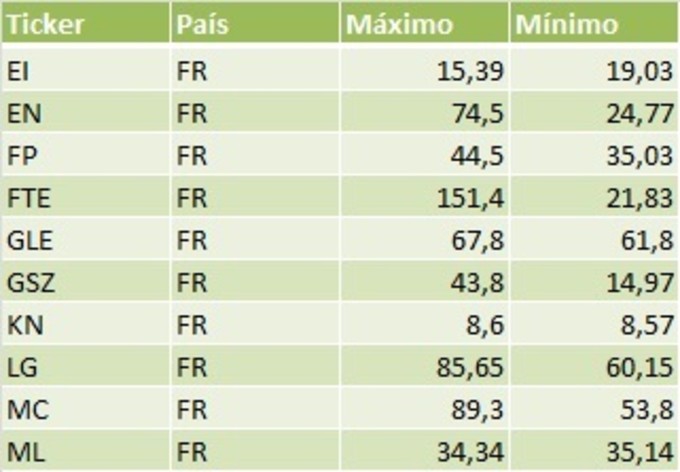tabla 1
- Calculamos las tablas de frecuencia individuales, así como las desviaciones respecto a la Ley de Benford
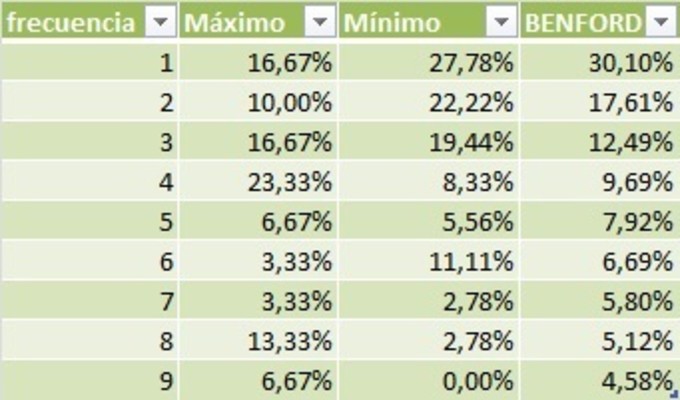tabla 2
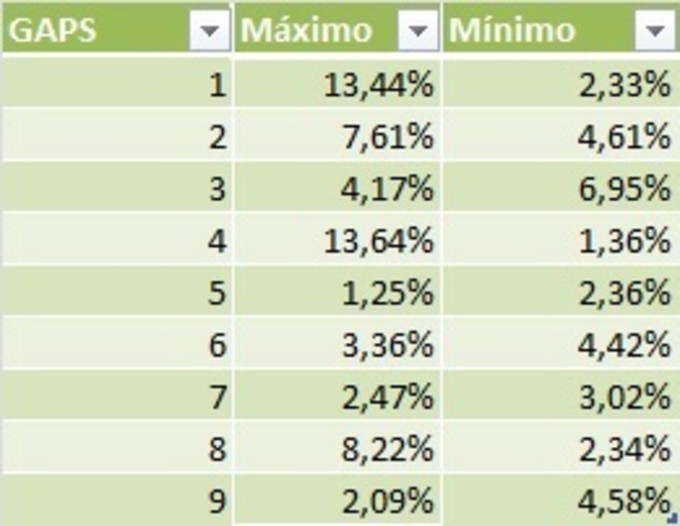tabla 3
- Calculamos las tablas de frecuencia agrupando por cifras
tabla 4
- Análisis, Interpretación y Apertura de Hipótesis
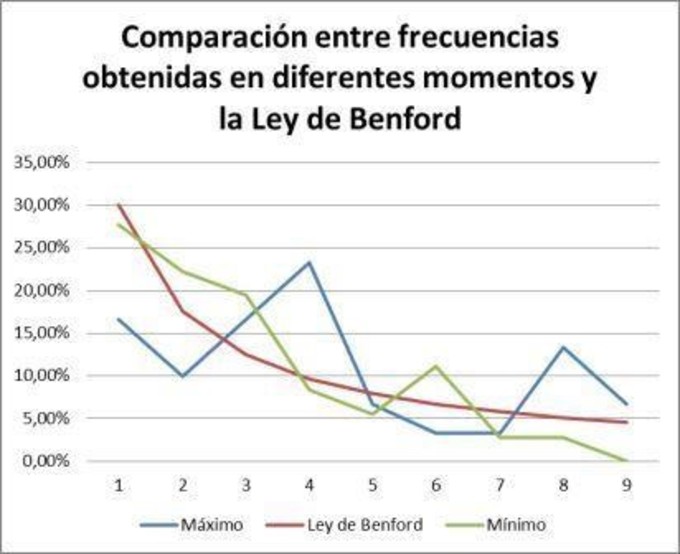
En el primero de los siguientes
gráficos muestro las frecuencias obtenidas en cada uno de los momentos y las de
la Ley de Benford (ver tabla 2). Podemos ver claramente que cuando el CAC 40 se
encontraba en mínimos la curva de frecuencias se ajusta mucho mejor a la
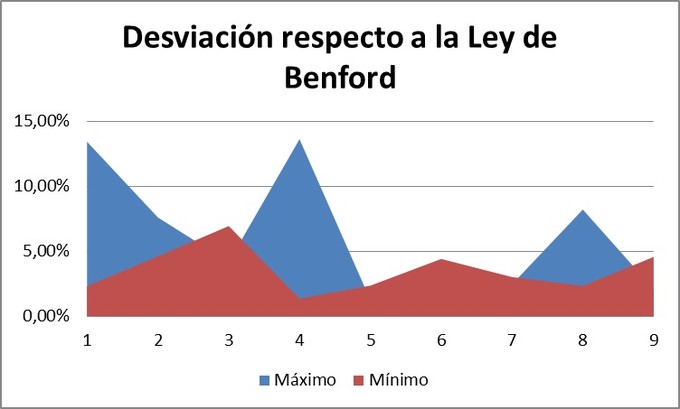
obtenida en máximos. Esto queda corroborado en el segundo gráfico, al
representar las desviaciones de las frecuencias con respecto a las de Benford (ver tabla 3). En la fecha de los máximos históricos, estos márgenes de
error son mucho más elevados que los obtenidos en la fecha de mínimos.
Una posible hipótesis podría
ser : “cuanto peor se ajuste la Ley de Benford a las frecuencias obtenidas en
un momento dado, más cerca estaré de un máximo. A su vez, cuanto mejor se ajuste
la Ley de Benford a las frecuencias obtenidas más cerca me encontraré de un
mínimo”.
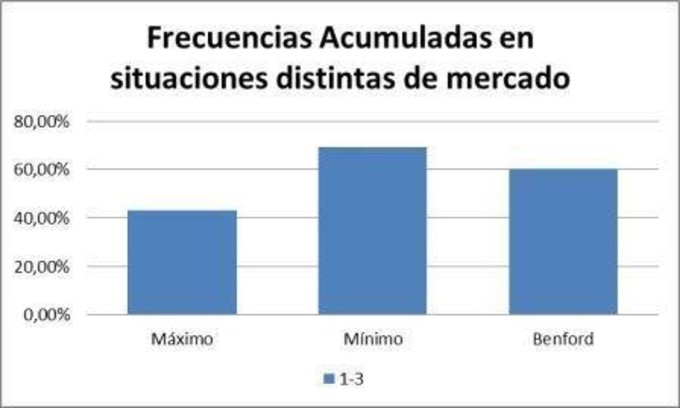
Por otro lado, he querido representar las frecuencias
acumuladas, dada la escasez de datos. Podemos ver que cuando el índice se encuentra en
máximos, las frecuencias se encuentran mucho más repartidas, mientras que
cuando el índice está en mínimos, son las cifras “1” a “3” las que aglutinan
mayor presencia (ver tabla 4).
En el gráfico siguiente observamos una mayor aparición de
las cifras “1” a “3” que las estipuladas por Benford, cuando el índice francés
se encontraba en mínimos. En contraposición, la frecuencia de aparición de
estas mismas cifras está muy por debajo de la probabilidad marcada por Benford,
cuando el índice se situaba en máximos.
De aquí otra posible
hipótesis : “A mayor aparición de las primeras cifras de nuestro sistema numérico en el primer dígito de los precios, mayor
situación de sobreventa está viviendo el Mercado”
O al revés : “A menor presencia de estas cifras en el
primer dígito de los precios, mayor situación de sobrecompra está viviendo el
Mercado”
Como ven, no expreso verdades irrefutables sino
hipótesis, pues nunca dispondremos de los suficientes datos, para demostrarlas (aunque cuantos más mejor). No obstante este estudio podría suponer un indicador como tantos otros que existen en análisis técnico.
El
experimento anteriormente realizado no es más que un ejemplo, quizás pueda
abrir la puerta a otras posibles ideas y aplicaciones de la Ley de Benford
para aproximarnos a los Mercados Financieros.
