En el primer artículo de esta serie se realizó una introducción a la inversión sistemática y se evaluó un modelo de "Comprar y Mantener" cada uno de estos ETFs por separado. En el segundo articulo se evaluó un modelo de cartera invertida 60% en SPY y 40% en TLT, rebalanceada mensualmente.
En este articulo evaluaremos una estrategia de rebalanceo periódico de pesos de activos en función de su riesgo. El objetivo es reducir la volatilidad total de la cartera y ver como afecta a la rentabilidad.
3) Estrategia 60/40 de asignación de pesos por riesgo.
Esta estratégia consiste en:
- Iniciamos la cartera calculando los pesos de SPY y TLT, de forma que el 60% del riesgo de la cartera quede asignado a SPY y el 40% del riesgo restante a TLT.
- El día 1 de cada mes, rebalanceamos los pesos de la cartera, de forma que el 60% del riesgo de la misma quede asignado a SPY y el 40% a TLT.
- Como medida de riesgo utilizaremos la volatilidad.
Este modelo es mas complicado que los anteriores, así que creo que es conveniente aclarar algunos conceptos respecto a riesgo y volatilidad.
¿ Que es riesgo y como se mide ?
En inversión, al igual que en el juego, podemos definir el riesgo como la pérdida de capital.
Es importante, por tanto, intentar medir y modelizar dicho riesgo para minimizar nuestras pérdidas de capital.
¿ Es volatilidad igual a riesgo ?
En general NO. La volatilidad es una medida de la frecuencia e intensidad de la variación del precio de un activo en un periodo de tiempo. Por si misma, mayor o menor volatilidad no implica direccionalidad en los precios, ya que en teoría un activo puede subir con mucho volatilidad y bajar con poco volatilidad (de hecho hay activos que se comportan así).
No obstante, debido a la asimetría de los mercados (que tienden a subir “ordenadamente” con baja volatilidad, y a caer rápidamente con alta volatilidad), y en activos suficientemente diversificados y con una distribución de los retornos aproximadamente normal (en sentido estadístico) es posible utilizar la volatilidad como proxy para el riesgo.
¿ Como se mide la volatilidad ?
Existen diversas maneras de medir la volatilidad, siendo la mas común utilizar la desviación estándar de los retornos. En este modelo utilizaremos como medida de volatilidad la desviación estándar de los retornos diarios, tomando para el cálculo un periodo de 21 días de cotización (correspondientes aproximadamente a un mes natural).
¿ Como funciona este modelo ?
Este modelo esta inspirado en la Teoría moderna de selección de cartera (modern portfolio theory) de Markowitz. Según esta teoría, bajo determinadas condiciones, podemos evaluar el riesgo de los activos en función de su volatilidad.
Un modelo clásico basado en esta teoría es el “equal risk” o “ risk parity", según el cual se calculan los pesos de los activos de forma que su contribución de riesgo a la cartera sea la misma.
Un modelo “equal risk" supondría asignar un 50% de contribución de riesgo a la cartera a cada uno de los ETFs, pero en vez de eso, vamos a desbalancear un poco las contribuciones de forma que SPY contribuya un 60% del riesgo a la cartera y TLT un 40%. De esta forma podremos comparar el comportamiento de una cartera con contribución 60%-40% en valor (articulo anterior) y en riesgo.
Al calcular los pesos de los activos en función del riesgo aportado y no del valor, lo que se consigue es que al aumentar el riesgo de un activo frente al otro, este vea reducido su peso en la cartera y viceversa, si se reduce el riesgo relativo, el activo verá aumentado su peso en la cartera. Esto debería reducir el riesgo de la cartera conjunta.
Ejemplo
- El valor de nuestra cartera es de $100.000 para el día 1/10/2014
- Calculamos la volatilidad, obteniendo para SPY una volatilidad anualizada de 9.3% y para TLT una volatilidad anualizada de 11.92%
- Con estos valores de volatilidad calculamos los pesos y obtenemos para SPY un peso de 65.75% y para TLT un peso de 34.25%. Comprobamos que (65.75*9.3) / (34.25*11.92) = 0.6 / 0.4
- Balanceamos los activos de nuestra cartera para tener $65750 de SPY y $34250 de TLT.
Rentabilidad
Llamaremos R_60_40 a nuestra cartera combinada 60% riesgo SPY y 40% riesgo TLT, rebalanceada mensualmente.
La rentabilidad acumulada de $1000 invertidos en R_60_40 al principio del periodo frente a la misma cantidad invertida en SPY y en la cartera V_60_40 del artículo anterior es
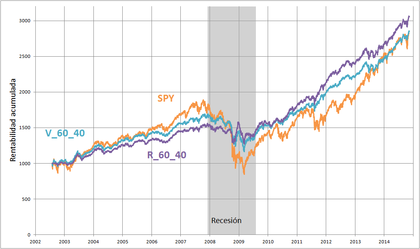
Siendo las rentabilidad anuales
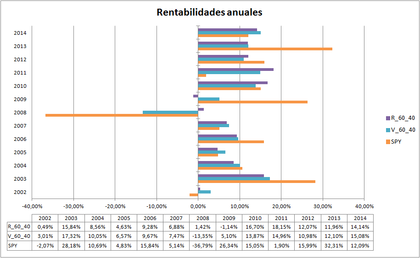
Podemos observar que, en periodos de baja volatilidad, la rentabilidad de R_60_40 es menor que las otras carteras, pero su comportamiento en periodos de alta volatilidad es muy bueno.
También es destacable que solo en el año 2009 hay rentabilidad negativa (-1.14%).
Riesgo y Drawdows
Calculando el riesgo y las rentabilidades, obtenemos
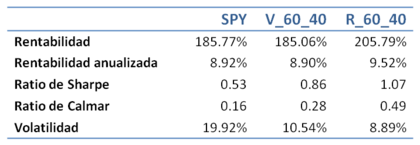
La rentabilidad ajustada al riesgo mejora frente a las otras carteras, obteniéndose una rentabilidad mayor asumiendo un menor riesgo, pero lo que más mejora es el ratio de Calmar, que tiene en cuenta los drawdowns.
Veamos pues los 5 mayores drawdowns, que serian
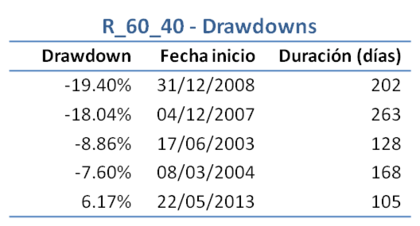
Los drawdown se reducen en intensidad y sobre todo en duración en comparación con las otras carteras. Lo mas destacable es que, entrando en el peor momento del mercado, el periodo de recuperación mas largo no llega a 9 meses, frente a periodos de dos y tres años en los otros modelos.
Conclusiones
El modelo reduce notablemente nuestro riesgo en comparación con los otros modelos, y no solo reduce la posible pérdida máxima de capital, sino que también reduce mucho el periodo de recuperación de dicha pérdida.
En el periodo completo, la rentabilidad acumulada es mayor en este modelo, y esto es debido al buen comportamiento en periodos de alta volatilidad como el periodo de recesión, pero hay que tener en cuenta que en periodos de baja volatilidad la rentabilidad es menor que los otros modelos.
Desde mi punto de vista es un modelo muy bueno: reduce el riesgo de la cartera y permite entrar o permanecer en el mercado incluso en momentos de gran incertidumbre, o después de subidas de mercado muy prolongadas como el actual.

