La idea que quiero transmitir en esta entrada es como podemos valorar una acción de una manera rápida como filtro para saber si en un principio es atractiva en precio, como accionistas, una empresa. Es un metódo básico para empresas maduras donde sus beneficios contables reflejen los beneficios reales, por lo que tendremos que fijarnos en sus flujos de caja e inversiones de mantenimiento y si mantienen una relación fiable con sus beneficios
El método que quiero desarrollar esta expuesto en el libro de Warren Buffett y la interpretación de los estados financieros y la idea es valorar una acción como un bono con cupón creciente.
La idea es tomar los beneficios contables antes de impuestos (income before taxes) y aplicarles un rendimiento como un bono para saber su precio P=(BPA/interes%). Está claro que para valorar de está forma tienen que ser empresas con ventajas competitivas que no sufran en exceso en las recesiones y sus beneficios sean como mínimo constantes, que es el fundamento de la fórmula, sin predecir futuros crecimientos que bienvenidos sean para la rentabilidad final porque nuestra rentabilidad desde el precio inicial de compra se irá incrementando según aumenten los beneficios.
En el siguiente caso de IBM se ve como los benéficios son volátiles y el valor oscila, lo que supone un problema importante para nuestra valoración.
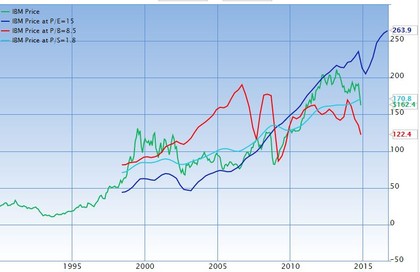
Fuente: Gurufocus
Para solucionar esto podemos normalizar los beneficios, en este caso lo he hecho con el ratio precio/ventas (linea azul P/S=1.8; 15=P/S*(1/Margen Neto)) y el margen neto medio de los últimos 10 años (12%), también podríamos normalizarlo con el roe medio 10 años por el valor contable por acción actual, obtengo el precio/ventas para un per de 15, que estimo similar al del mercado porque tiene una beta de 0.9 respecto a este, aunque podríamos permitir un poco más (Beta<1) si preferimos ser conservadores, además su histórico verifica este valor medio, tiene riesgo similar al mercado ya que este número (beta) nos da una medida de la volatilidad del precio respecto al mercado en general (riesgo), y por consiguiente de sus beneficios ya que la mayor parte de las veces las cotizaciones siguen la tendencia de los beneficios a no ser en valoraciones exageradas donde se han descontado crecimientos que no se han materializado, de ahí que en el libro se expone que con un ratio precio/beneficios mayor a 40 es mejor colocar nuestro dinero en bonos del tesoro ya que una recesión acabará llegando y obtendremos buenos precios de compra, así que vale más pájaro en mano.
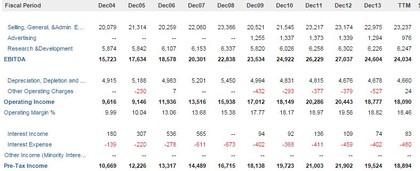
Fuente: Gurufocus
Después de desviarme un poco del tema con ratios seguimos con la valoración como si se tratara de un bono donde el cupón son los beneficios antes de impuestos, esto es así porque si nuestra inversión fuera en bonos la rentabilidad es también antes de impuestos, esta forma seria la correcta, pero si queremos ser conservadores tomamos el beneficio neto después de impuestos de las operaciones continuas sin extras que será menor.
Normalizo los beneficios, el margen de los beneficios antes de impuestos medio de los últimos 10 años es del 17% si lo multiplico por las ventas actuales, 98014 (mil) $, me da 16662 (mil) $ ahora finalmente obtengo los beneficios por acción (diluidas=998 (miles)) 16662/998=16.69 $/acción este es nuestro cupón.
Finalmente nos resta aplicarle el interés, aquí podemos tomar dos caminos:
1.- Aplicar la rentabilidad de los bonos corporativos de IBM con vencimiento en ¡¡2096!! 4.46%, Warren dice que el precio de las acciones es como si se tratase de un bono de cupón creciente, a largo plazo el precio sigue el rendimiento de sus bonos corporativos.
2.- Ser conservadores y aplicar una rentabilidad de 9.52% correspondiente a la rentabilidad media histórica de IBM=> Aplicando un tipo impositivo del 30% a los beneficios antes de impuestos (BAI), los beneficios después de impuestos son un 70% (E=BAI x (1-0.3)) lo que nos daría un múltiplo equivalente de 10.5 (P/BAI=P/E x E/BAI=15 x 0,7=10.5) antes de impuestos tomando un múltiplo P/E medio de 15 al que le correspondería un interés equivalente de 1/10.5=0.095
Caso 1: 16.69/0.0446=374.21 $ parece un precio por acción un poco desorbitado ya que sería aplicarle un ratio PER de 1/0.0446=22 nunca visto en esta compañía en los últimos 10 años.
Caso 2: 16.69/0.095= 175 $ por acción mucho más razonable y con un descuento del precio actual.
Si nos fijamos en el primer gráfico del ratio P/S=1.8, vemos como la cotización histórica se ajusta bien si empleamos el beneficio neto después de impuestos (170$/acción), pero si nos atenemos a la formula es antes de impuestos, lo que siempre nos reporta un precio por acción algo mayor dependiendo del tipo impositivo. A si que lo que podemos sacar como conclusión es que IBM esta entre correctamente valorada y barata (-10%) y que dada su rentabilidad (ROE >50%) seguirá creciendo lo que nos da un margen de seguridad más amplio ya que crea valor ( ROE-Coste de capital accionista >0) y estaremos dispuestos a pagar una prima por su valor en libros de 8.55 veces (57%/6.66%)[3]que es el ratio P/VC
Notas
[1] Libro:
http://www.amazon.es/Warren-Buffett-interpretaci%C...
http://books.google.es/books?id=NKQYd_9Ljh4C&print...
[2] Una fórmula con la que hoy en día es difícil encontrar valores infravalorados a no ser en recesiones donde podemos tomar ventaja del trato dado a los precios que no reflejan la calidad del negocio, es la expuesta por Benjamin Graham quien decía que una empresa estaría correctamente valorada si su Precio/Valor tangible contable era igual a 1.5 y su PER igual a 15 o que una combinación de ambas fuese equivalente a esos valores, de ahí se puede obtener lo suiguiente.
Precio=1.5 x VC ; Precio=15 x BPA => si sumo a ambos lados de la igualdad 2xPrecio=1.5xVC+15 x BPA
Precio=1.5/2x VC+15/2 x BPA => Precio=0.75* VC + 7.5 x BPA
[3] Precio/Valor Contable= ROE medio 10 años / Coste de capital accionista
Este artículo no pretende ser una recomendación de compra sólo pretende tener un objetivo didáctico

